Quantum Computers: Flipping Coins and Killing Cats
In October, following leaks, secrecy and scepticism, a short
paper was finally released online by the journal Nature. In it, researchers at
Google claimed to have achieved “quantum supremacy.” They stated they had
performed a computation that would take 10,000 years to complete with the
world’s best supercomputer, but which only took them a few minutes on a new type of device
called a quantum computer. To achieve this, the team at Google had to imprint a
tiny network of superconductors on a computer chip, cool it to thousandths of a
degree above the lowest temperature physically possible, and manipulate every
component of the device with minimal error in concert with the rest of the chip. This was no mean feat. In the Nature paper where this achievement is recorded, Google christened the device
“Sycamore.”
A Chat With a Quantum Superstar
A few weeks ago, one of the heads of Google’s quantum research, John Martinis, was discussing ideas for Sycamore’s
future with some of the professors and postdocs working in the same research
group as me. I had no practical reason for being there, but you don’t just give
up the opportunity to meet a celebrity in your field, so I managed to convince
the professor in charge to let me sit in on the meeting. Meeting Martinis was
somewhat anticlimactic – my interaction with him was limited to a handshake,
after which I was seated in the corner, listening lamely as incomprehensible
terms were being flung across the coffee table. But the bits I picked up were
enough to paint a picture of the Google research effort and of the man Martinis
himself.
He’s a tall, thin figure with a mop of thick, grey hair slapped rather chaotically onto his head, allowing him to nicely reflect our shared picture of a genius physicist. He came across as an affable and enthusiastic character who, perhaps as a consequence of the Californian start-up culture, oozed an easy-going confidence. It was the tacit assumption that Sycamore was the best in the world at everything it was capable of doing. And the things it couldn't do yet? Well it'll get there pretty shortly.
He’s a tall, thin figure with a mop of thick, grey hair slapped rather chaotically onto his head, allowing him to nicely reflect our shared picture of a genius physicist. He came across as an affable and enthusiastic character who, perhaps as a consequence of the Californian start-up culture, oozed an easy-going confidence. It was the tacit assumption that Sycamore was the best in the world at everything it was capable of doing. And the things it couldn't do yet? Well it'll get there pretty shortly.
This portrait of poise and smiles was a little undercut,
however, whenever rival players in the quantum game were mentioned. You see, Google isn't the only company investing in quantum computing. IBM, Microsoft, Lockheed Martin and a raft of others are collectively sinking millions into the field, all wanting to develop the most powerful quantum machines. At one point in the conversation, when discussing the limited access that some other
companies provide to their own devices, Martinis asked conspiratorially “I
mean, what are they hiding?”
Clearly there is a little bad air between the quantum companies.
This was probably exacerbated by a recent paper released by IBM researchers,
which turned out to be a bit of a thorn in the side of Google’s quantum supremacy claims. The
idea of quantum supremacy is that if you have a large enough quantum computer
that you have sufficient control over, you can do things that would take an
enormous amount of time on a normal computer. When this length of time becomes
ridiculous, people say that we have achieved quantum supremacy. Google claimed
that, for the first time, their quantum computer performed a task that would take the world’s best
supercomputer 10,000 years to complete. IBM, meanwhile, claimed that it would
actually only take 2.5 days on that supercomputer. Of course Google, in turn, struck back with their own rebuttal. However the fact that IBM's paper came out before
Google’s original was even officially released, somewhat took the wind out of the sails of this result.
Beyond these debates of quantum supremacy, there are two points that lie at the centre of the quantum race. The first is the
concept of benchmarking – the varied set of approaches to testing how much
control you have over your quantum device. Essentially, if a quantum computer
is an extremely slippery bar of soap, benchmarking provides an answer to the
question: how well can you hold onto it? Benchmarking allows one company to
make a quantitative claim that their quantum computer is “better” than all the
others. The other concept is “quantum error correction,” which is sometimes
thought of as the holy grail of quantum computing – the achievement that will
allow these devices to revolutionise the world. Whoever is able to implement
quantum error correction in a large-scale manner will unlock the powers that
quantum computers promise us.
In these articles, I want to explore the concepts that surround this burgeoning field. In this post and the ones to come, I'm going to be illustrating the ideas behind quantum algorithms, benchmarking and error correction, as I think this will provide an understanding of the mind-boggling and controversial world of quantum computing research. However to start off with, we’ll have to understand the principles on which these devices are based: the physics of quantum mechanics. This topic alone is enough to fill textbooks and
completely fry your brain, so it will be enough to fill up this first article. But
after establishing the ground work, we'll be able to turn to the other topics
sparking debates and excitement. The second post will give an intuitive picture of how quantum computers work, while the next will explain why discussions of benchmarking happening outside of the media
spotlight could be much more important for the field than minor scraps over supercomputer run times. Finally, I’ll address what all the fuss is about with
quantum error correction. We’ll look at how it works, and how it will push the bounds of quantum computer capabilities and of currently-established
science. At the end I’ll touch on how it might even provide insight into the
fundamental nature of space and time.
But first, we’ll start more modestly, with a look at the
brain-frying microscopic world of quantum mechanics.
Quantum What Now?
Every
popular article on quantum computing breakthroughs mentions the number of
“qubits” that a new device has. But what puts the “q” in qubit, and how can that
secret ingredient generate $405 million in private funding over just two years?
Here’s the spiel given by most popular descriptions of
quantum computing: normal computers work by storing information as strings of
0’s and 1’s, so-called binary digits or “bits.” For example a number, say 50, could be represented as the string of bits 110010. But a quantum computer stores
information as quantum bits, “qubits,” which can be both a 0 and a 1 at the
same time. This is most famously demonstrated in the Schrödinger's Cat thought experiment, where a cat in a box can be both alive and dead before it is observed. Because of this phenomenon, called superposition, quantum computers can perform certain tasks
exponentially faster than their classical (which just means non-quantum) cousins.
At this point most of us tend to glaze over and say “Uhuh”.
But we shouldn’t say “uhuh”! We should say: “What?! That doesn’t make any sense! 0 and 1? Alive and dead? What are you talking about? And how does
that logic-defying rubbish make something exponentially faster?” It’s fair to
say that we should expect more from these explanations.
This isn’t to say that the right explanation won’t be
confusing. "Quantum" is synonymous with confusion. Most of the time, rather than getting
lost in difficult questions, physicists end up just saying “uhuh” to the
universe, a sentiment summed up by the mantra “shut up and calculate.” But I
think here we can at least do better than the “0 and 1 at the same time” handwaving. However, if you find
yourself getting confused, that probably means you’re on the right track, so hang in
there. Ready? Good, let’s get started.
What's a Qubit?
Physically, a qubit could be anything, so long as it’s isolated enough from its surroundings. All you need for a system to be given the illustrious title “qubit” is for it to be in one of two possible states. So for example if your qubit is a cat, the two states could be “standing up” or “sitting down” (this cat has a slightly brighter future than Schrodinger’s). For practical purposes though, you need your system to be very small. So for example, you might be dealing with a single atom or a single particle of light, or an electron, or a tiny piece of superconductor. Each of these can be thought of as a tiny coin, which can be showing either heads or tails.
Suppose this coin is sitting on a desk, with either the heads or tails side showing. This desk is very tall, and what's more you're blindfolded, so in order to see which face is showing you ask your good friend, who’s recently been bitten by a radioactive spider, to hop up on the ceiling and take a look. He says that the coin is in the heads position. But standing next to the desk at head height, you know without looking that if you took off your blindfold, all you'd be able to see is the coin’s edge. According to you, the coin isn’t in either the heads nor the tails position.
But now you actually look at the coin. And here comes the first difficult pill to swallow. If you look at the coin which is neither heads nor tails, it instantaneously changes its orientation so that it now faces you. And what do you see on the coin? Heads or tails? The answer is, it’s completely random – it’s impossible to predict what you will see with certainty, even with complete knowledge of the state of the universe.
This means that if I look at the coin and see heads, I could look at it again a moment later and see it
having spontaneously flipped to tails. Here’s how:
But the strange part is that I can look at my coin when it’s in this non-heads, non-tails state and I will see heads or tails. I’ll change the orientation of the coin just by measuring it.
This opens a whole philosophical can of worms. What does “measurement” actually mean? Does the 50/50-ness of the outcome mean that the world is inherently non-deterministic? All of these questions have no universally accepted answers. But for now, we’ll just say that “measurement” is whatever we have to do to force the coin to show us either heads or tails. In an actual laboratory, it might involve shining light on an atom, passing an electron through a magnetic field, or a particle of light through a crystal. But we don’t want to get bogged down in these details, so it pays to be just a little bit hand-wavy about these things.
This means that if I look at the coin and see heads, I could look at it again a moment later and see it
having spontaneously flipped to tails. Here’s how:
- I look at the coin and see heads.
- I ask spidey to look at the coin. The coin has its edge facing him initially, so it’s neither heads nor tails according to him. But when he looks, it spontaneously pops into a heads or tails position. But now the coin is in an undetermined state according to me.
- I look at the coin again. The result will be completely random, so with 50% probability I will see tails where first I saw heads.
This is definitely very weird. Just by looking at this quantum coin in a choreographed way, we can get it to change its configuration. You might think this is just like if I flipped the coin. I’d have a 50% probability of seeing tails, nothing special. And maybe it is like that. Maybe we do have to think about “looking” at something as being like flipping a coin. The thing is, we don’t really know. We have no idea how this process of looking at things actually works – a conundrum known as the measurement problem of quantum mechanics. All we know is that looking at something (or to use the jargon, “measuring” something) inherently involves changing the state of that thing.
And, by the way, when the coin has its edge facing me we say that the coin is in a “superposition” of heads and tails. All this means is that measuring the coin face could give either heads or tails. When people say a qubit is “a 0 and a 1 at the same time” they mean it is in a superposition of the two states, so measuring its value could give 0 or 1. But this seems a bit of a strange choice of language from the coin perspective, where being in a superposition of heads and tails meant it had its edge facing me. It’s better to think about superposition meaning that the coin is oriented in such a way that the question “is it heads or tails” isn’t really sensible.But the strange part is that I can look at my coin when it’s in this non-heads, non-tails state and I will see heads or tails. I’ll change the orientation of the coin just by measuring it.
This opens a whole philosophical can of worms. What does “measurement” actually mean? Does the 50/50-ness of the outcome mean that the world is inherently non-deterministic? All of these questions have no universally accepted answers. But for now, we’ll just say that “measurement” is whatever we have to do to force the coin to show us either heads or tails. In an actual laboratory, it might involve shining light on an atom, passing an electron through a magnetic field, or a particle of light through a crystal. But we don’t want to get bogged down in these details, so it pays to be just a little bit hand-wavy about these things.
Superposition and Measurement
Now we’ll see that we can do away with spidey and still have this measurement weirdness. Imagine I have a fat coin with a thick edge. I paint half of that edge black and the other half white. I can now ask the question “what colour is the edge facing me?” just as before I could ask the question “which side, heads or tails, is facing me?" And just as before, if I start with a coin in the position heads, and “measure” the edge colour, it will spontaneously pop into the orientation with either the black edge or the white edge facing me.But now the concept of superposition is forced on us. If I see heads, I can't say whether a black or a white edge is facing me (after all, there's no edge facing me at all), and were I to measure the edge colour it would show black or white with 50% probability. And similarly if it's in a black-edge state, I could measure either heads or tails with 50% probability. The coin is always in a superposition according to either the edges or the faces.
One feature of a superposition is that, no matter what state the coin is in, I can always say something about the edge colours (and the faces). For example, have a look at the above (terribly drawn) picture. If I can see the head oriented upright I know that the black edge is on the left and the white edge is on the right. So I can say something about the particular arrangement of edge colours, even when I see a face like heads. So the edges are always in a definite state. If the coin is in a heads state, I could describe it equally validly as being in a black-on-the-left state (assuming the head is oriented the right way up). This all means that there are two ways of describing the same state of the coin. This concept of switching between the face-description and the edge-description is known as a “change of basis.” The heads/tails option is one basis – one way of describing the state of the coin – and the black-left/black-right description is another one. And just to hammer the message home, when the coin is in a heads state (or equivalently a black-left state), measuring its edge colour will provide black or white with 50% probability, so it is in a superposition of these two outcomes. And we could always choose something to measure (face or edge for example) that is undetermined. The quantum world forces superposition and randomness on us.
Entanglement
There is now one last ingredient we need before we can understand the power of quantum computing. This last phenomenon is called entanglement. We can understand it through the coin analogy again. If I now have two coins, there are four possible states the pair can be in: $hh$, $ht$, $th$ or $tt$. They could of course be in superpositions of these states as well, but as we saw before, we can describe superpositions using different arrangements of these basis states. So the four basis states are the tools we have to play with to describe our system.
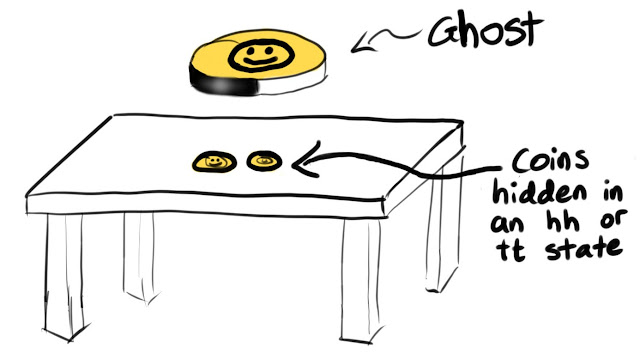
Now imagine we put these two coins on a table in the $hh$ state and cover them up with a cloth, before calling it a day with our coin games, content in our perfect knowledge of our two coins. Then in the dead of night, while we’re dreaming of coins in $h$ positions, along comes some quantum hacker who has a bit of a fiddle with the coins on our table. When we come back to the table the next morning, the hacker informs us that she’s changed the state of the coins. We no longer have perfect knowledge. But she gives us a bit of solace by telling us that the coins are definitely not in the states $ht$ or $th$. They are only in either the state $tt$ or $hh$. We are slightly appeased, because the hacker has reduced our uncertainty a little bit. All we need to do is look at one coin now, and we will have perfect knowledge of the pair. If I take a peak below the cloth and see the left coin is $h$, the right coin must also be $h$.
After hearing the hacker’s information, it’s now as if our pair of coins was really just one single bigger coin that swallows up the two original ones. Let’s call it the ghost coin of the original pair, since it’s not actually real. If the small coins are in the $hh$ state, we interpret the ghost coin as being in the heads state ($H$). And if the small coins are in the $tt$ state, we say the ghost coin is in the tails state ($T$).
Now things get a bit abstract. Let’s imagine we paint the edges of this ghost coin white and black, in the same way as we did before with the physical coins. Now what happens if we put the ghost coin in an edge state, say with black facing us? Well we associate this with a certain combination of $H$ and $T$, like we did before. We say that the ghost is in the state which has $T$ on the left and $H$ on the right, for example. That means the real coins are somehow in a combination of $hh$ and $tt$. But if we measure one of these small coins, and see $h$ for example, we will instantly know that the other coin is in the $h$ state as well, because the hacker has told us that they will always show the same face. So the real coins are in an indeterminate state, some fuzzy combination of $hh$ and $tt$, and yet I only need to measure one of them to have actually measured both of them. And because measurement involves change, measuring one coin changes the state of the other instantly, no matter how far separated they are.
This is by far the strangest aspect of quantum mechanics. Systems, like coins, can be talking with one another in a certain way, so that we have to describe them with a single larger system, the "ghost," whose state is given by the two smaller coins. And because of this ghost, when we measure coin A we also change the state of coin B, even though we never touched it! This phenomenon, in which we have to use a ghost to describe a collection of systems, is called entanglement.
More generally, if I have several coins entangled together in a certain way, I can describe that using a ghost as well. But with more coins we can have more possible outcomes when they are entangled. For example if I have four coins, the hacker could specify that they are either $hhhh$, $hhtt$, $tthh$, or $tttt$. This particular state can be thought of as two ghost coins, since there are four possible outcomes. With even more physical coins it’s better to think of the ghost as a die with many sides.
We are not forced to combine our coins into the die in a fixed way. Going back to our single ghost coin example, we could think of the ghost as being weighted or biased, so that when we measure it, we see heads 80% of the time and tails 20% of the time. One of the important ways quantum computers achieve a speedup relative to classical computers is by manipulating these probabilities. The idea is to boost the probability of finding the “right answer” when you make a measurement of the ghost. We’ll get into the details of how this works in the next post.
Now imagine we put these two coins on a table in the $hh$ state and cover them up with a cloth, before calling it a day with our coin games, content in our perfect knowledge of our two coins. Then in the dead of night, while we’re dreaming of coins in $h$ positions, along comes some quantum hacker who has a bit of a fiddle with the coins on our table. When we come back to the table the next morning, the hacker informs us that she’s changed the state of the coins. We no longer have perfect knowledge. But she gives us a bit of solace by telling us that the coins are definitely not in the states $ht$ or $th$. They are only in either the state $tt$ or $hh$. We are slightly appeased, because the hacker has reduced our uncertainty a little bit. All we need to do is look at one coin now, and we will have perfect knowledge of the pair. If I take a peak below the cloth and see the left coin is $h$, the right coin must also be $h$.
After hearing the hacker’s information, it’s now as if our pair of coins was really just one single bigger coin that swallows up the two original ones. Let’s call it the ghost coin of the original pair, since it’s not actually real. If the small coins are in the $hh$ state, we interpret the ghost coin as being in the heads state ($H$). And if the small coins are in the $tt$ state, we say the ghost coin is in the tails state ($T$).
Now things get a bit abstract. Let’s imagine we paint the edges of this ghost coin white and black, in the same way as we did before with the physical coins. Now what happens if we put the ghost coin in an edge state, say with black facing us? Well we associate this with a certain combination of $H$ and $T$, like we did before. We say that the ghost is in the state which has $T$ on the left and $H$ on the right, for example. That means the real coins are somehow in a combination of $hh$ and $tt$. But if we measure one of these small coins, and see $h$ for example, we will instantly know that the other coin is in the $h$ state as well, because the hacker has told us that they will always show the same face. So the real coins are in an indeterminate state, some fuzzy combination of $hh$ and $tt$, and yet I only need to measure one of them to have actually measured both of them. And because measurement involves change, measuring one coin changes the state of the other instantly, no matter how far separated they are.
This is by far the strangest aspect of quantum mechanics. Systems, like coins, can be talking with one another in a certain way, so that we have to describe them with a single larger system, the "ghost," whose state is given by the two smaller coins. And because of this ghost, when we measure coin A we also change the state of coin B, even though we never touched it! This phenomenon, in which we have to use a ghost to describe a collection of systems, is called entanglement.
More generally, if I have several coins entangled together in a certain way, I can describe that using a ghost as well. But with more coins we can have more possible outcomes when they are entangled. For example if I have four coins, the hacker could specify that they are either $hhhh$, $hhtt$, $tthh$, or $tttt$. This particular state can be thought of as two ghost coins, since there are four possible outcomes. With even more physical coins it’s better to think of the ghost as a die with many sides.
We are not forced to combine our coins into the die in a fixed way. Going back to our single ghost coin example, we could think of the ghost as being weighted or biased, so that when we measure it, we see heads 80% of the time and tails 20% of the time. One of the important ways quantum computers achieve a speedup relative to classical computers is by manipulating these probabilities. The idea is to boost the probability of finding the “right answer” when you make a measurement of the ghost. We’ll get into the details of how this works in the next post.
What's Going on Here?
This is all strange and confusing so let's take stock of what we know so far. Qubits form the fundamental units of information in a quantum computer. These are like the bits (0's and 1's) used to store information in a classical computer, but now we have to think of these qubits as tiny coins. There are various ways of describing the state of one of these coins. It can be described using the faces (heads or tails) or the edge colours (white or black). If the coin is in a definite state according to one basis, it will be in a superposition of the states of a different basis. So for example, a coin in the $h$ state will be in the superposition described as "black-on-the-left" according to the edge colour basis. If you measure the coin when it's in a superposition, it spontaneously pops into one of the two possible outcomes, decided completely at random. For example, measuring the edge colour of a coin in the $h$ state will result in black or white with 50% probability.
When I have multiple coins, I can place them in a superposition of their combined states (such as $hhhh$, $hhht$, etc.). This corresponds, in our analogy, to describing the entire system with a large ghost die whose faces give the various measurement outcomes (such as $hhhh$). The probability of rolling any given face can be specified by me. For example, with four coins there are 16 basis states. But we could place them in a superposition of $hhhh$, $hhtt$, $tthh$, $htht$, $thth$ and $tttt$. To describe this state we need a 6-sided ghost die. We could adjust the weighting of this die so that we roll $hhhh$ with 50% probability, and the rest with 10% probability each.
These coins and ghosts embody the fundamental concepts needed to understand the workings of a quantum computer. But let's go back to what they represent. Remember a qubit could be anything, in principle. For example, it could be a particle of light, a photon. You might remember from school that light involves the electromagnetic field wiggling in a certain way. Photons are the smallest amount of wiggle that you can have while still having any light at all. They come in two polarisations, horizontal or vertical, corresponding to the direction that the light is wiggling in (polarised sunglasses work by letting through one of these polarisations and blocking the other).
To think of the photon as a qubit, we think of the vertical polarisation as the $h$ state and the horizontal polarisation as the $t$ state. If we have two photons, they could be entangled so that they are forced to wiggle in the same direction. Measuring one photon's polarisation forces the other to be the same. To emphasise how strange this is, the two photons could be on opposite ends of the universe. But measuring one will still change the state of the other instantaneously, as if they were somehow connected despite their immense separation.
How do these weird properties allow us to perform tasks exponentially faster on a quantum computer? And how do we manipulate the information stored in these qubits? I'll explain all this and more in the next few posts (see the next post here). But if you want to have a think about why quantum bits might be superior to classical ones, ponder the following:
When I have multiple coins, I can place them in a superposition of their combined states (such as $hhhh$, $hhht$, etc.). This corresponds, in our analogy, to describing the entire system with a large ghost die whose faces give the various measurement outcomes (such as $hhhh$). The probability of rolling any given face can be specified by me. For example, with four coins there are 16 basis states. But we could place them in a superposition of $hhhh$, $hhtt$, $tthh$, $htht$, $thth$ and $tttt$. To describe this state we need a 6-sided ghost die. We could adjust the weighting of this die so that we roll $hhhh$ with 50% probability, and the rest with 10% probability each.
These coins and ghosts embody the fundamental concepts needed to understand the workings of a quantum computer. But let's go back to what they represent. Remember a qubit could be anything, in principle. For example, it could be a particle of light, a photon. You might remember from school that light involves the electromagnetic field wiggling in a certain way. Photons are the smallest amount of wiggle that you can have while still having any light at all. They come in two polarisations, horizontal or vertical, corresponding to the direction that the light is wiggling in (polarised sunglasses work by letting through one of these polarisations and blocking the other).
To think of the photon as a qubit, we think of the vertical polarisation as the $h$ state and the horizontal polarisation as the $t$ state. If we have two photons, they could be entangled so that they are forced to wiggle in the same direction. Measuring one photon's polarisation forces the other to be the same. To emphasise how strange this is, the two photons could be on opposite ends of the universe. But measuring one will still change the state of the other instantaneously, as if they were somehow connected despite their immense separation.
How do these weird properties allow us to perform tasks exponentially faster on a quantum computer? And how do we manipulate the information stored in these qubits? I'll explain all this and more in the next few posts (see the next post here). But if you want to have a think about why quantum bits might be superior to classical ones, ponder the following:
- Suppose you had two qubits entangled with the probabilities: 10% for $hh$, 40% for $ht$, 20% for $th$ and 30% for $tt$. How many bits would you need to store these probabilities, assuming from the outset that each basis state's probability is a multiple of 10%? You might want to do this if you were simulating the workings of a quantum computer on a classical computer. (Hint: Encode 0% through 100% as a string of 0's and 1's of a certain length. You can do this four times, once for each of the four different basis states.) How many bits would be needed to store the probabilities for a four-coin state? Can you see why it might be hard to simulate the workings of a quantum computer using classical bits?











Comments
Post a Comment