Quantum Algorithms: Squashing the Exponential
In 1828, a twelve-year-old girl decided that she wanted to fly. She was being looked after by her Governess at the time, while her mother was away receiving treatment for one of her commonly recurring illnesses. While thinking about that immense distance between her and her only remaining parent, it occurred to her. If she were able to fly, she could visit her mother wherever she was in the world in almost no time at all! There was a slight problem though: nobody had ever been able to fly before. No matter, she thought. She would simply have to invent a method of flying all on her own. Powered by a stubborn sense of determination, she set herself to the task of studying the anatomy of birds, then gathered some tools and began constructing a machine to send her into the air. This was a scientific project, and as such it would involve a great deal of experimentation. She cycled through different materials and altered the shape and size of the wings to try to imitate the successful strategy that nature had pioneered. Her idea was to attach this set of wings to a steam engine that would power the flight. Her design, while rudimentary, was the first of its kind. It preceded a patent for an "aerial steam carriage" by about 15 years, and the Wright Brothers' first flight by 75 years.
The girl's name was Ada Byron, later known as Ada Lovelace. Her father was the notorious bad-boy poet, Lord Byron, who had died of fever just a few years before Ada designed her flying machine. But Ada hadn't seen the man since she was a month old and instead was raised by her mother, Annabella, when she wasn't being treated away from home. Terrified that Ada might have inherited her father's poetical mind, along with his "madness," Annabella had her daughter educated on a strict diet of mathematics and science, to instill in her some mental fortitude. While it was this technical education that allowed Ada to design her flying machine, it was perhaps a little bit of poetic imagination that gave her the idea to do so. Maybe her mother hadn't been quite so successful after all.
The design of Ada's machine might crudely be thought of as an algorithm. An algorithm is simply a set of precise instructions that allows one to complete a particular task in a finite period of time. While algorithms have been developed for thousands of years, it wasn't until the invention of the computer that they began to be studied rigorously. As Ada grew up, the focus of her algorithms shifted from tasks carried out by humans to those carried out by machines, and in so doing, she became entwined in the beginnings of the science of computation that would blossom over the coming century. Several years after her pictures of a flying machine had been placed at the bottom of a drawer, Ada would write an algorithm to be run on a theoretical new device called the analytical machine, designed by Charles Babbage. This algorithm is considered by many to be the first ever computer program. From that invention we can trace a line through Alan Turing, Bill Gates, the iPhone and onward, into a world in the 21st Century in which computers and the algorithms that tell them how to run are everywhere. But this first program was designed simply to generate sets of numbers that were hard to calculate, a fairly dry mathematical task. Ada's brilliance - maybe another result of a technical mind imbued with a little poetry - was in foreseeing the true capabilities of computers. She thought of them not as number crunchers, but as symbol processors, potentially capable of one day interpreting text, drawing graphics and maybe even composing music. We live in a world in which each of these insights has become a reality.
As can be seen from this foresight, although they've grown immensely in their capabilities, the logic underlying the workings of today's computer algorithms is the same as the logic Ada was working with almost two centuries ago. In the last post we talked about how quantum mechanics provides a world where logic seems to act quite differently to what we expect, and I promised that the result of this world would be a device on which problems could be solved exponentially faster than they can on your laptop. In this post we'll follow through on this promise to properly get an understanding of how a quantum computer works. We'll focus on one algorithm in particular, going through the principles behind how it works, in order to hopefully gain some intuition for the capabilities of quantum computation. This will hint at why, given access to a large-scale quantum computer, we could expect new insights into almost all areas of science and technology, opening up a whole world of knowledge.
Let's start by condensing some of the many words used in the last post. Notation, though it may look daunting, can help us de-clutter everything. Remember the picture we had in mind of a qubit being a tiny coin with its edge painted half white and half black. We introduced two basis sets for this coin: heads, tails and white, black. If we see a face, it must be either $h$ or $t$ and if we see an edge it must be either $w$ or $b$. If I want to say that the coin is in the $h$ state, the way I am going to write that is using some strange brackets: $|h\rangle$.
But we can equally validly describe a coin in the $|h\rangle$ state using the other basis, whose states are $|w\rangle$ and $|b\rangle$. Remember, I could say that $h$ is equivalent to a certain arrangement of the edges, namely the arrangement "black edge on the left." We used the term "superposition" to describe this phenomenon. In our new notation, we do the same thing and say that the $h$ state is equivalent to the $w$ and $b$ states combined in a certain way, and we indicate this concept by whacking a $+$ sign between the two edge states, like this: $|h\rangle = \frac{1}{\sqrt{2}}|b\rangle + \frac{1}{\sqrt{2}}|w\rangle$. The reason we include a $\frac{1}{\sqrt{2}}$ in front of each state in the superposition has to do with probabilities. If you take the number out the front of a state and square it, you get the probability of finding that state if you were to perform a measurement. So in the above, each of $|b\rangle$ and $|w\rangle$ has a probability of 1/2 or 50% of being measured. I'll often omit these square roots in the notation whenever the exact probabilities don't matter. So what about the $t$ state? We said that $t$ was equivalent to the arrangement "black edge on the right" and we indicate that by subtracting the two edge states: $|t\rangle = \frac{1}{\sqrt{2}}|b\rangle - \frac{1}{\sqrt{2}}|w\rangle$. This addition and subtraction isn't like the addition or subtraction of numbers; instead it just represents a way of combining the two states, $|b\rangle$ and $|w\rangle$, to a form a new state. Something to notice is that due to this notation, the state $|h\rangle$ can be thought of as "kind-of-$b$" and "kind-of-$w$" at the same time. This is like saying North-West is kind of North and kind of West at the same time. That's the essence of superposition.
When we have more than one coin, we can combine the state of all coins into a single set of brackets, such as $|hhh\rangle$, which indicates three coins all in the $h$ state. The number of combinations of states increases as we increase the number of coins. For example, we could have a state $$\begin{align*} &\frac{1}{\sqrt{8}}|hhh\rangle + \frac{1}{\sqrt{8}}|hht\rangle + \frac{1}{\sqrt{8}}|hth\rangle + \frac{1}{\sqrt{8}}|htt\rangle \\ +&\frac{1}{\sqrt{8}}|thh\rangle + \frac{1}{\sqrt{8}}|tht\rangle + \frac{1}{\sqrt{8}}|tth\rangle + \frac{1}{\sqrt{8}}|ttt\rangle \end{align*}$$ which is a superposition of all possible states of three coins. Using the ideas introduced last time, the way we think about a state like this is as an eight-sided "ghost die," where each face of the die represents a single arrangement of coins, and the probability of rolling any face is 1/8.
We'll start by sticking with the coins analogy, just for a bit of fun. In reality logic gates are mathematical operations, but we'll get into that later. Imagine I have lots of coins setup on a table, all heads up, and in a cage on one end I have a mouse, who happens to have a hankering for peanut butter. Now on one of my coins, say the last one, I smear some of her favourite brand of peanut-based spread on the tails side. So if I open the cage, the mouse will run along the table and leave all the coins alone apart from the last one, which she will flip upside down to get at the peanut butter. The mouse has thereby changed the information stored in the coins. This is the idea of a logic gate – a very basic manipulation of stored information. In this case, our logic gate changes the string $(h,h,h,h,\ldots ,h)$ to $(h,h,h,h,\ldots ,t)$. This type of gate is called a NOT gate, because the state of the last coin is "not" what it was initially - that is, the coin is flipped over.
None of this sounds very quantum yet. But what if we put one of these coins in superposition? Suppose I paint the edges of my coins again, and if I want to put one of them in a superposition of heads and tails, I place it on its edge, with either the black or white side facing left. I’ll do this in a careful way, such that if the coin was initially heads, I’ll put it in the black-left position, $|b\rangle$. And if it was initially tails, I’ll put it in the white-left position, $|w\rangle$. This is actually a gate in itself, called a Hadamard gate. The action of this gate is to alter a coin's state in this way: $$|h\rangle \rightarrow |b\rangle , \quad |t\rangle \rightarrow |w\rangle .$$
Suppose that a mysterious stranger hands you a stack of cards. These cards have a dark side and a light side. The light sides of the cards have all the numbers from 1 to some very large number, say 8192 – each card with its own number. Whereas the dark sides each have an unknown number. Being a curious, scientifically minded individual, you want to find out what’s on the dark side of the cards. But you are also a very busy (or lazy?) individual and don’t have time to check the back of every card to satiate your curiosity. What do you do?
Let’s make some further assumptions. We’ll assume that you have access to a few things, namely coins and a mouse (naturally), and a very clever assistant. You begin by asking your assistant to make a machine, using the coins and mouse provided, that can give you the number on the dark side of a card when you provide it with the number on the light side. So if I fed the number 42 into the machine, encoded in the state of some coins, it would spit out whatever number is on the dark side of card 42. It doesn’t matter how this machine is made, but you can imagine it being composed from the elementary logic gates we looked at above.1
Now comes the clever part. You have the ability to represent each number between 1 and 8192 in the coins on your table (incidentally, you’ll need 13 coins in order to do this). You would encode this information by letting $1 = (h,h,h,\ldots,h,h)$, $2 = (h,h,h,\ldots,h,t)$, $3 = (h,h,h,\ldots,t,h)$, $4 = (h,h,h,\ldots,t,t)$, etc. Then if you fed one of these coin arrangements into the machine, you would receive back another arrangement of coins, this time encoding the number on the dark side of the card you requested. If you wanted all dark side numbers and were determined to use the given coins classically, you'd have to send in all 8192 light side numbers.
But what if you were willing to flirt with the quantum? What if you placed all the coins on their edges? What is this state? Well if you slammed your hand on top of each coin (thereby measuring each coin's state in the $h$, $t$ basis), you’d get a random string of $h$’s and $t$’s, which represents one of your numbers from 1 to 8192. You could have measured any of those 8192 numbers, and there was an equal probability of measuring any one of them. That means the state with each coin on its edge represents a superposition of all possible numbers. Or, alternatively, it is represented by a 8192-sided unbiased ghost die.
Now if you feed this superposition into the machine, you are effectively feeding in all of the 8192 light side numbers at the same time, thereby requesting the values of all dark sides at once. In one shot you get the answer to all of your 8192 questions! The output of the machine will be a superposition as well, also represented by a ghost die. We can think of the result as the machine changing the weighting of the ghost die. If four dark sides have the number 100 while only one has the number 1, the ghost die spat out of the machine is four times as likely to roll a 100 as it is to roll a 1. In this way, all of your answers are encoded in the weightings of the ghost.
But there’s a problem. How do we access these weightings? If you measure your state by rolling the die, you will find only one number, which will be chosen at random from the list of possible options. And once you roll the die, your state is altered irreparably (remember performing a measurement changes the state). So you can only roll the die once. This gives you the dark side of only one card, chosen at random, and you could have got that by just using the machine in the classical way, feeding coins in facing either heads or tails up. It seems like our quantum bits are no more useful than our classical bits.
But let's not be so hasty. Maybe we can still get some understanding of the global features of the dark side numbers. We won’t walk away with a full list of those numbers, but we might still be able to find out some useful information, like how clumped together or spread out the numbers are, or maybe whether or not they repeat themselves after a certain number of cards.
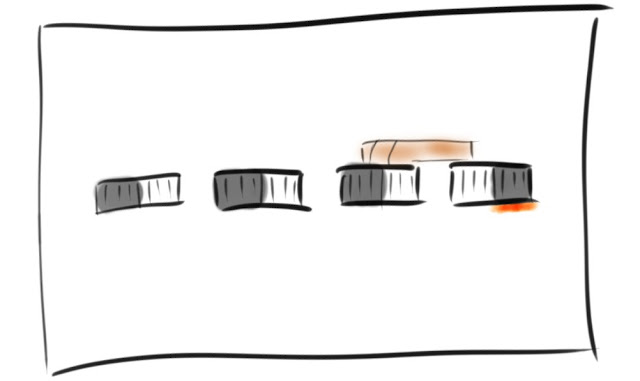
Suppose we send a superposition of 0 and 2 into our QFT. What the QFT does is it sets the hand moving at 1 tick per second (t.p.s.) and it takes a series of photos of the clockface, at times specified by the input. So in this example it takes photos of the clockface at the 0 second and the 2 second marks. It then superimposes these two images. Then it does the same thing but for the speed of 2 ticks per second. Again, it takes photos at the 0 second and 2 second marks and superimposes them. It repeats this procedure for all speeds up to 8 t.p.s. Now for most speeds we will find two copies of the hand in each image, at different locations. But at the speed of 4 t.p.s. the hand completes one full revolution every two seconds, and so the second photo is taken when the hand is sitting where it started. So the superimposed photo for the speed of 4 t.p.s. will only have one image of the hand in it. (This will also happen for the speed of 8 t.p.s.) These images of the clock face represent numbers, complex numbers in fact,2 and they modify the probabilities associated with each state in the superposition. We can therefore write the output of the QFT schematically as:
What do these clock face images actually tell us about the various probabilities though? Well the key fact is that the probability of measuring a particular speed decreases as the clock face image associated with it looks more blurry. If the hand appears in many locations around the clockface in the image, that is an unlikely speed to measure, whereas if it appears in a tight concentration around one point, that is a much more likely speed to measure. In the above example, we are less likely to measure speeds whose pictures have two hands than we are to measure speeds whose pictures only have one copy of the hand. In fact we have zero probability of measuring 2 t.p.s. above, because the hands pictured are directly opposite each other.
Now let's be a bit more ambitious and use more numbers. We'll send in a superposition of, for example, 0, 4, 8, 12, etc. all the way up to some very large number - might as well use 8192 again. In this case, the period is 4. Then any speed that results in some number of full revolutions of the hand every 4 seconds (i.e. 1/4, 1/2, 3/4 or 1 full revolution per second), will only produce one image of the hand and thus be much more probable to measure than any other speed. In general, we are very likely to measure the speed of $k/r$ revolutions per second, for some random number $k$, where remember that $r$ is the period. By the way, this corresponds to $8192k/r$ ticks per second. So we measure a number $8192k/r$, where $k$ and $r$ are both unknown. But it turns out that with some clever guessing and checking, we can actually find the number $r$ that we are after very efficiently!
It's important to note how much better this is than if we hadn't used the QFT. If we'd done nothing but measure the input state - rolling that unbiased 8192-sided ghost die - we would've had to make a huge number of measurements before we had any good estimate of what the period was. But with the QFT, with high probability, we only have to make one measurement! Okay but who cares? Well, as promised, this mathematical tool is the cornerstone of one of the first and most famous quantum algorithms, known as...
https://www.chattyfeet.com/blogs/chattyfeet-socks-blog/ada-lovelace-facts-first-programmer
http://cs-exhibitions.uni-klu.ac.at/index.php?id=345
https://www.computerhistory.org/babbage/adalovelace/
The girl's name was Ada Byron, later known as Ada Lovelace. Her father was the notorious bad-boy poet, Lord Byron, who had died of fever just a few years before Ada designed her flying machine. But Ada hadn't seen the man since she was a month old and instead was raised by her mother, Annabella, when she wasn't being treated away from home. Terrified that Ada might have inherited her father's poetical mind, along with his "madness," Annabella had her daughter educated on a strict diet of mathematics and science, to instill in her some mental fortitude. While it was this technical education that allowed Ada to design her flying machine, it was perhaps a little bit of poetic imagination that gave her the idea to do so. Maybe her mother hadn't been quite so successful after all.
The design of Ada's machine might crudely be thought of as an algorithm. An algorithm is simply a set of precise instructions that allows one to complete a particular task in a finite period of time. While algorithms have been developed for thousands of years, it wasn't until the invention of the computer that they began to be studied rigorously. As Ada grew up, the focus of her algorithms shifted from tasks carried out by humans to those carried out by machines, and in so doing, she became entwined in the beginnings of the science of computation that would blossom over the coming century. Several years after her pictures of a flying machine had been placed at the bottom of a drawer, Ada would write an algorithm to be run on a theoretical new device called the analytical machine, designed by Charles Babbage. This algorithm is considered by many to be the first ever computer program. From that invention we can trace a line through Alan Turing, Bill Gates, the iPhone and onward, into a world in the 21st Century in which computers and the algorithms that tell them how to run are everywhere. But this first program was designed simply to generate sets of numbers that were hard to calculate, a fairly dry mathematical task. Ada's brilliance - maybe another result of a technical mind imbued with a little poetry - was in foreseeing the true capabilities of computers. She thought of them not as number crunchers, but as symbol processors, potentially capable of one day interpreting text, drawing graphics and maybe even composing music. We live in a world in which each of these insights has become a reality.
As can be seen from this foresight, although they've grown immensely in their capabilities, the logic underlying the workings of today's computer algorithms is the same as the logic Ada was working with almost two centuries ago. In the last post we talked about how quantum mechanics provides a world where logic seems to act quite differently to what we expect, and I promised that the result of this world would be a device on which problems could be solved exponentially faster than they can on your laptop. In this post we'll follow through on this promise to properly get an understanding of how a quantum computer works. We'll focus on one algorithm in particular, going through the principles behind how it works, in order to hopefully gain some intuition for the capabilities of quantum computation. This will hint at why, given access to a large-scale quantum computer, we could expect new insights into almost all areas of science and technology, opening up a whole world of knowledge.
A Little Notation
But we can equally validly describe a coin in the $|h\rangle$ state using the other basis, whose states are $|w\rangle$ and $|b\rangle$. Remember, I could say that $h$ is equivalent to a certain arrangement of the edges, namely the arrangement "black edge on the left." We used the term "superposition" to describe this phenomenon. In our new notation, we do the same thing and say that the $h$ state is equivalent to the $w$ and $b$ states combined in a certain way, and we indicate this concept by whacking a $+$ sign between the two edge states, like this: $|h\rangle = \frac{1}{\sqrt{2}}|b\rangle + \frac{1}{\sqrt{2}}|w\rangle$. The reason we include a $\frac{1}{\sqrt{2}}$ in front of each state in the superposition has to do with probabilities. If you take the number out the front of a state and square it, you get the probability of finding that state if you were to perform a measurement. So in the above, each of $|b\rangle$ and $|w\rangle$ has a probability of 1/2 or 50% of being measured. I'll often omit these square roots in the notation whenever the exact probabilities don't matter. So what about the $t$ state? We said that $t$ was equivalent to the arrangement "black edge on the right" and we indicate that by subtracting the two edge states: $|t\rangle = \frac{1}{\sqrt{2}}|b\rangle - \frac{1}{\sqrt{2}}|w\rangle$. This addition and subtraction isn't like the addition or subtraction of numbers; instead it just represents a way of combining the two states, $|b\rangle$ and $|w\rangle$, to a form a new state. Something to notice is that due to this notation, the state $|h\rangle$ can be thought of as "kind-of-$b$" and "kind-of-$w$" at the same time. This is like saying North-West is kind of North and kind of West at the same time. That's the essence of superposition.
When we have more than one coin, we can combine the state of all coins into a single set of brackets, such as $|hhh\rangle$, which indicates three coins all in the $h$ state. The number of combinations of states increases as we increase the number of coins. For example, we could have a state $$\begin{align*} &\frac{1}{\sqrt{8}}|hhh\rangle + \frac{1}{\sqrt{8}}|hht\rangle + \frac{1}{\sqrt{8}}|hth\rangle + \frac{1}{\sqrt{8}}|htt\rangle \\ +&\frac{1}{\sqrt{8}}|thh\rangle + \frac{1}{\sqrt{8}}|tht\rangle + \frac{1}{\sqrt{8}}|tth\rangle + \frac{1}{\sqrt{8}}|ttt\rangle \end{align*}$$ which is a superposition of all possible states of three coins. Using the ideas introduced last time, the way we think about a state like this is as an eight-sided "ghost die," where each face of the die represents a single arrangement of coins, and the probability of rolling any face is 1/8.
Logic Gates
How can a hunk of inert matter process information and deliver an outcome that is intelligible to humans? If we’re clever, we might be able to represent things of interest, from numbers to videos of cats, as very specific arrangements of coins on a table. For example, I could specify that $hh = 0$, $ht = 1$, $th = 2$ and $tt = 3$, thereby representing information (in this case one of four possible numbers) using pieces of metal. But representing information is not enough to make a computer. We need to be able to manipulate the information too. To do this, we need to find a way to implement something called a logic gate.We'll start by sticking with the coins analogy, just for a bit of fun. In reality logic gates are mathematical operations, but we'll get into that later. Imagine I have lots of coins setup on a table, all heads up, and in a cage on one end I have a mouse, who happens to have a hankering for peanut butter. Now on one of my coins, say the last one, I smear some of her favourite brand of peanut-based spread on the tails side. So if I open the cage, the mouse will run along the table and leave all the coins alone apart from the last one, which she will flip upside down to get at the peanut butter. The mouse has thereby changed the information stored in the coins. This is the idea of a logic gate – a very basic manipulation of stored information. In this case, our logic gate changes the string $(h,h,h,h,\ldots ,h)$ to $(h,h,h,h,\ldots ,t)$. This type of gate is called a NOT gate, because the state of the last coin is "not" what it was initially - that is, the coin is flipped over.
What other manipulations can I get my mouse to make? Well suppose I smear peanut butter on the underside of the second coin, but then I tape a ruler to the heads side of the first. This ruler sticks out and covers the second coin, like so:
Now these are heavy coins so the mouse can’t lift more than one of them at a time. So when the first coin is heads up (Case 1), the ruler covers the second coin and our mouse can’t flip it over to get at the peanut butter. But when the first coin is tails up (Case 2), the ruler is on the underside of the second coin, and so the mouse can flip it to get at the peanut butter. So whether or not our mouse flips the second coin is dependent on the state of the first. This type of gate is called a Controlled-NOT (CNOT for short), since the "NOT action" is controlled by the state of the first coin.
None of this sounds very quantum yet. But what if we put one of these coins in superposition? Suppose I paint the edges of my coins again, and if I want to put one of them in a superposition of heads and tails, I place it on its edge, with either the black or white side facing left. I’ll do this in a careful way, such that if the coin was initially heads, I’ll put it in the black-left position, $|b\rangle$. And if it was initially tails, I’ll put it in the white-left position, $|w\rangle$. This is actually a gate in itself, called a Hadamard gate. The action of this gate is to alter a coin's state in this way: $$|h\rangle \rightarrow |b\rangle , \quad |t\rangle \rightarrow |w\rangle .$$
Now we have extra logical manipulations available to us. I can, for example, put some peanut butter on half of the coin, say coating the half of the coin with the black edge (see the left-hand side of the figure below). Then, when the mouse eats it, the pressure of her nose will cause the coin to spin from the black-left position to the black-right position, changing it from $|b\rangle$ to $|w\rangle$. If I now go back and take the coins out of superposition, reversing the action of the Hadamard gate, I’ll place this swivelled coin down tails-up where it was initially heads-up.
We can appreciate the novelty of these quantum coins when considering what happens when I place a ruler on the first coin so that it covers the second, then I place the two coins in superposition, shown in the right-hand side of the figure above. Now what happens if I place peanut butter on the black side of the second coin? Well if the black side is to the left, then when the mouse eats the peanut butter off the second coin, she will cause it to swivel. But now the ruler gets in the way, so she ends up causing both coins to swivel, changing the state of the first as well.
But if the black side is to the right, as in the above figure, the mouse will cause the second coin to swivel the other way and the first coin will be unaffected. So now the state of the first coin after the mouse passes will be dependent on the state of the second. But beforehand, when the coins were lying flat, it was the other way around! This is a fundamentally quantum mechanical phenomenon. The ruler stuck to the first coin means that, in the $|h\rangle$, $|t\rangle$ basis, the second coin gets flipped dependent on the state of the first, whereas in the $|b\rangle$, $|w\rangle$ basis, the first coin gets flipped dependent on the state of the second!
Understanding this through the notation we've introduced is quite simple when we understand that the "ruler," or the CNOT gate, acts like something multiplying the state. It is defined by its action on a particular basis of two qubits as follows: $$\text{CNOT}|hh\rangle = |hh\rangle , \; \text{CNOT}|th\rangle = |tt\rangle , \; \text{CNOT}|ht\rangle = |ht\rangle , \; \text{CNOT}|tt\rangle = |th\rangle .$$
That is, the second qubit is flipped whenever the first is in the $t$ state and left alone otherwise. If we write its action in the other basis, it looks like this: $$\text{CNOT}|bb\rangle = |bb\rangle , \; \text{CNOT}|bw\rangle = |ww\rangle , \; \text{CNOT}|wb\rangle = |wb\rangle , \; \text{CNOT}|ww\rangle = |bw\rangle .$$ Just as we saw with the ruler and mouse, in this basis the first coin's state is flipped whenever the second coin is in the $w$ state and left alone otherwise. All this is to say that logic gates in quantum computers are much slipperier than their classical counterparts, and quantum algorithms that take advantage of this slipperiness can do things that are not possible on classical computers. Now that we've got a feel for the bare units of quantum computation, we can start to build a picture of the broader principles at play in the algorithms we're interested in.
We now have a nice analogy and also a mathematical description for how a quantum computer might work. We have a bunch of coins to represent information, a peanut-butter-loving mouse to manipulate that information, and an ability to measure the state of the coins. Or, using the jargon, we have a collection of qubits and logic gates. So where does this famed exponential speedup come from? We can get a feel for how a quantum computer might perform faster than its classical counterpart using an idea known as quantum parallelism. Quantum Parallelism
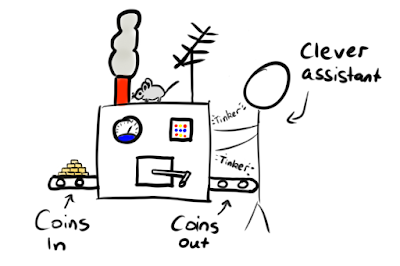
Suppose that a mysterious stranger hands you a stack of cards. These cards have a dark side and a light side. The light sides of the cards have all the numbers from 1 to some very large number, say 8192 – each card with its own number. Whereas the dark sides each have an unknown number. Being a curious, scientifically minded individual, you want to find out what’s on the dark side of the cards. But you are also a very busy (or lazy?) individual and don’t have time to check the back of every card to satiate your curiosity. What do you do?
Let’s make some further assumptions. We’ll assume that you have access to a few things, namely coins and a mouse (naturally), and a very clever assistant. You begin by asking your assistant to make a machine, using the coins and mouse provided, that can give you the number on the dark side of a card when you provide it with the number on the light side. So if I fed the number 42 into the machine, encoded in the state of some coins, it would spit out whatever number is on the dark side of card 42. It doesn’t matter how this machine is made, but you can imagine it being composed from the elementary logic gates we looked at above.1
Now comes the clever part. You have the ability to represent each number between 1 and 8192 in the coins on your table (incidentally, you’ll need 13 coins in order to do this). You would encode this information by letting $1 = (h,h,h,\ldots,h,h)$, $2 = (h,h,h,\ldots,h,t)$, $3 = (h,h,h,\ldots,t,h)$, $4 = (h,h,h,\ldots,t,t)$, etc. Then if you fed one of these coin arrangements into the machine, you would receive back another arrangement of coins, this time encoding the number on the dark side of the card you requested. If you wanted all dark side numbers and were determined to use the given coins classically, you'd have to send in all 8192 light side numbers.
But what if you were willing to flirt with the quantum? What if you placed all the coins on their edges? What is this state? Well if you slammed your hand on top of each coin (thereby measuring each coin's state in the $h$, $t$ basis), you’d get a random string of $h$’s and $t$’s, which represents one of your numbers from 1 to 8192. You could have measured any of those 8192 numbers, and there was an equal probability of measuring any one of them. That means the state with each coin on its edge represents a superposition of all possible numbers. Or, alternatively, it is represented by a 8192-sided unbiased ghost die.
Now if you feed this superposition into the machine, you are effectively feeding in all of the 8192 light side numbers at the same time, thereby requesting the values of all dark sides at once. In one shot you get the answer to all of your 8192 questions! The output of the machine will be a superposition as well, also represented by a ghost die. We can think of the result as the machine changing the weighting of the ghost die. If four dark sides have the number 100 while only one has the number 1, the ghost die spat out of the machine is four times as likely to roll a 100 as it is to roll a 1. In this way, all of your answers are encoded in the weightings of the ghost.
But there’s a problem. How do we access these weightings? If you measure your state by rolling the die, you will find only one number, which will be chosen at random from the list of possible options. And once you roll the die, your state is altered irreparably (remember performing a measurement changes the state). So you can only roll the die once. This gives you the dark side of only one card, chosen at random, and you could have got that by just using the machine in the classical way, feeding coins in facing either heads or tails up. It seems like our quantum bits are no more useful than our classical bits.
But let's not be so hasty. Maybe we can still get some understanding of the global features of the dark side numbers. We won’t walk away with a full list of those numbers, but we might still be able to find out some useful information, like how clumped together or spread out the numbers are, or maybe whether or not they repeat themselves after a certain number of cards.
Quantum Fourier Transform
Let's investigate this last feature a bit more closely, in which the dark side numbers are periodic. Imagine the deck of cards we were given had dark side numbers that followed a repeating pattern. So after a certain number of cards we would be back to where we started. Let's call this number the period, and denote it $r$. So the dark side of the 1st card would be the same as that of the $(r+1)$th card and the $(2r + 1)$th card and so on. After we send the coins (turned on their sides) into the machine, this number $r$ is encoded in the superposition that the machine spits back out again. But how do we access it? You might ask why we would want to access it. Well it turns out that finding this number for a certain deck of cards is at the heart of one of the most famous quantum algorithms, which may threaten to break the security protocols our computers use every day. We'll discuss this algorithm below, but first we need to talk about how we actually find this piece of the jigsaw.
The tool needed for finding the period of a superposition is the Quantum Fourier Transform (QFT). The normal Fourier Transform is a mathematical trick that allows you to take in a waveform pattern, like a note played on a violin, and generate all the frequencies that make up that sound. The QFT is similar, except it takes in a state, like one represented by coins on a table, and generates a set of “frequencies” that produce that state. This is a bit abstract, but bear with me.
A way of understanding how this procedure works is by imagining that all the numbers we're dealing with are arranged around a clockface, with a single hand ticking around the face (in the counter-clockwise direction just to keep you on your toes). To make it simple, we'll just deal with numbers from 0 to 7.
The output states of the QFT correspond to speeds with which the hand ticks. In general, the output of the QFT might be a superposition of all possible speeds: 1 tick per second, 2 ticks per second, and so on, up to 8 ticks per second. But the weights or probabilities of measuring any particular speed in the output may vary. Let's see how that works.
The tool needed for finding the period of a superposition is the Quantum Fourier Transform (QFT). The normal Fourier Transform is a mathematical trick that allows you to take in a waveform pattern, like a note played on a violin, and generate all the frequencies that make up that sound. The QFT is similar, except it takes in a state, like one represented by coins on a table, and generates a set of “frequencies” that produce that state. This is a bit abstract, but bear with me.
A way of understanding how this procedure works is by imagining that all the numbers we're dealing with are arranged around a clockface, with a single hand ticking around the face (in the counter-clockwise direction just to keep you on your toes). To make it simple, we'll just deal with numbers from 0 to 7.
The output states of the QFT correspond to speeds with which the hand ticks. In general, the output of the QFT might be a superposition of all possible speeds: 1 tick per second, 2 ticks per second, and so on, up to 8 ticks per second. But the weights or probabilities of measuring any particular speed in the output may vary. Let's see how that works.
What do these clock face images actually tell us about the various probabilities though? Well the key fact is that the probability of measuring a particular speed decreases as the clock face image associated with it looks more blurry. If the hand appears in many locations around the clockface in the image, that is an unlikely speed to measure, whereas if it appears in a tight concentration around one point, that is a much more likely speed to measure. In the above example, we are less likely to measure speeds whose pictures have two hands than we are to measure speeds whose pictures only have one copy of the hand. In fact we have zero probability of measuring 2 t.p.s. above, because the hands pictured are directly opposite each other.
Now let's be a bit more ambitious and use more numbers. We'll send in a superposition of, for example, 0, 4, 8, 12, etc. all the way up to some very large number - might as well use 8192 again. In this case, the period is 4. Then any speed that results in some number of full revolutions of the hand every 4 seconds (i.e. 1/4, 1/2, 3/4 or 1 full revolution per second), will only produce one image of the hand and thus be much more probable to measure than any other speed. In general, we are very likely to measure the speed of $k/r$ revolutions per second, for some random number $k$, where remember that $r$ is the period. By the way, this corresponds to $8192k/r$ ticks per second. So we measure a number $8192k/r$, where $k$ and $r$ are both unknown. But it turns out that with some clever guessing and checking, we can actually find the number $r$ that we are after very efficiently!
It's important to note how much better this is than if we hadn't used the QFT. If we'd done nothing but measure the input state - rolling that unbiased 8192-sided ghost die - we would've had to make a huge number of measurements before we had any good estimate of what the period was. But with the QFT, with high probability, we only have to make one measurement! Okay but who cares? Well, as promised, this mathematical tool is the cornerstone of one of the first and most famous quantum algorithms, known as...
Shor's Algorithm
We're finally ready to introduce an actual quantum algorithm. Unfortunately this is going to be a rather hand-wavy introduction because the specifics would take too long to go into. But those specifics that we're going to avoid don't have anything to do with quantum mechanics, so you'll hopefully come away with an understanding of the important quantum aspects of this algorithm.
The idea is to find the prime factors of a
very large number. While multiplying two numbers together is very
easy on a computer, going in the reverse direction is very difficult. You can
demonstrate this for yourself on your calculator. Multiply 59 and 67 together.
It’s very quick, it doesn’t really feel like you’ve done much at all. Now take the
number 9379 and tell me what the prime factors are (the prime numbers that
divide it evenly). All you can do is guess primes and check if they are factors. It’s
a very tedious task!
The number of guesses you need in order to
find the prime factors of a number $N$ grows exponentially in the number of digits of $N$. Computers rely on this difficulty for encryption. Having the
prime factors of a large number is like having a key to a piece of online
information. The computer gives you the large number $N$, and if you can provide it with a prime factor of $N$ you can access the
information. This allows information to be seen only by the intended recipient
who has the key.
But a quantum computer can factor a large $N$ in a run-time that grows as a polynomial in the number of digits of $N$. That is, if we double the number of digits of $N$, the run-time would double or quadruple or octuple etc. depending on the exact polynomial we are dealing with. While this seems bad, this is exponentially faster than any known classical algorithm. This means
that a large enough quantum computer could feasibly find the prime factors of very large numbers in
a reasonable amount of time, and thereby break internet encryption. Let's see how this algorithm works.
The procedure, devised by Peter Shor in 1994, essentially comes down to finding certain patterns in a collection of numbers. Earlier we were talking about packs of cards with light side and dark side numbers. Well I didn't say this explicitly, but each pack of cards actually represents a mathematical function - a rule for getting from the light side number to the dark side number. In this case we're interested in the following rule:
The procedure, devised by Peter Shor in 1994, essentially comes down to finding certain patterns in a collection of numbers. Earlier we were talking about packs of cards with light side and dark side numbers. Well I didn't say this explicitly, but each pack of cards actually represents a mathematical function - a rule for getting from the light side number to the dark side number. In this case we're interested in the following rule:
- Start with a random number, $a$, which is less than $N$, the number we want to factorise.
- Take your light side number and raise $a$ to the power of that number.
- Divide the result by $N$ and then look at the remainder. This is your dark side number.
For an example, let's use $N = 9$ and $a = 4$. If the light side number on one card is 5, we look at $4^5 = 1024$, and divide that number by 9. The result is 113 with a remainder of 7, so 7 is the dark side number for the 5th card. This procedure is known as modular exponentiation - the 'modular' bit just refers to this deal about finding remainders. It turns out that with this procedure or function dictating the backs of our cards, the dark side numbers have a period associated with them, $r$. That is, they repeat after every $r$ cards. In the case of $N=9$ and $a=4$ the period is $r=3$, since if we start with 0, $4^{0}=1$ and $4^3=64$, and 9 goes into 64 7 times with a remainder of 1, which is where we started. It turns out that for a general $N$, if we can work out $r$, assuming we haven't accidentally made a dumb choice for $a$, we can very easily find a prime factor of $N$. It's worth stressing this because it's not at all obvious. When we look at the results of this modular exponentiation procedure, we find that the outputs repeat after $r$ input numbers. And if we can find $r$, we can very easily produce a prime factor of $N$. This is pretty amazing! But there's a catch. Finding $r$ is very hard. On a classical computer, we are once again stuck with guessing and checking. But if we have a quantum computer at our disposal, we're in luck, because we've just discussed a tool that can help us find the period of a set of numbers: the Quantum Fourier Transform!
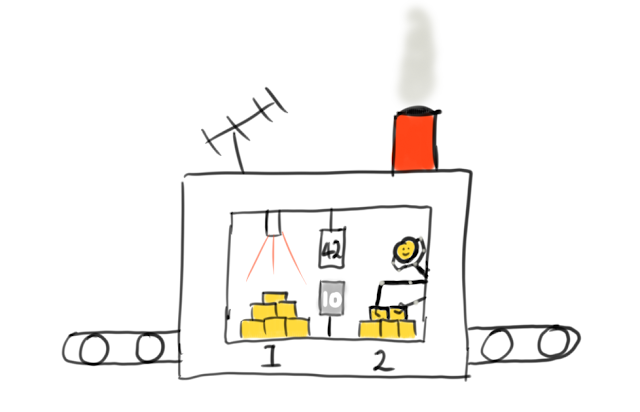
The quantum algorithm then goes as follows. Start with two sets of coins (or qubits if you want to be all technical). Guess a random number $a$ which is less than $N$. Then make a machine using your clever assistant, peanut butter and mouse (or logic gates if you have a peanut allergy) which reads the state of the coins in set 1, treats that as a light side number, then imprints the corresponding dark side number onto the state of the coins in set 2, where the dark side number is the result of the modular exponentiation stuff we just talked about. So if we send through the number 42 in set 1, and 10 is on the dark side of the 42nd card, then the output of the machine will be set 1 in the 42-state and set 2 in the 10-state.
Now before sending anything through this machine, place the coins in set 1 on their edges. This represents a state which is a superposition of all possible numbers from 0 up to some very large number. Just leave set 2 as it is, in the 0-state if you like, then send both through the machine. After this, the two sets will be entangled. From last post, remember that this means that if I do a measurement on set 1, I instantly know what the state of set 2 is. Namely, if I measure set 1 to be in the $x$-state, I know that set 2 will be in the $y$-state, where $y$ is the dark side number of card $x$.
The quantum algorithm then goes as follows. Start with two sets of coins (or qubits if you want to be all technical). Guess a random number $a$ which is less than $N$. Then make a machine using your clever assistant, peanut butter and mouse (or logic gates if you have a peanut allergy) which reads the state of the coins in set 1, treats that as a light side number, then imprints the corresponding dark side number onto the state of the coins in set 2, where the dark side number is the result of the modular exponentiation stuff we just talked about. So if we send through the number 42 in set 1, and 10 is on the dark side of the 42nd card, then the output of the machine will be set 1 in the 42-state and set 2 in the 10-state.
Now before sending anything through this machine, place the coins in set 1 on their edges. This represents a state which is a superposition of all possible numbers from 0 up to some very large number. Just leave set 2 as it is, in the 0-state if you like, then send both through the machine. After this, the two sets will be entangled. From last post, remember that this means that if I do a measurement on set 1, I instantly know what the state of set 2 is. Namely, if I measure set 1 to be in the $x$-state, I know that set 2 will be in the $y$-state, where $y$ is the dark side number of card $x$.
But what if instead I choose to measure set
2? Suppose I find some value $y$ at random. Well, because the dark side numbers repeat themselves, there are multiple set 1 numbers that could
have produced this outcome, all separated by the period $r$. The first set of coins must be in a superposition of all of
these values. Let’s call the smallest of these values $x$. So set 1 is in a superposition of $x$, $x+r$, $x+2r$, and so on. If, for example, $x$ is 5 and $r$ is 10, set 1 would be in a superposition of 5, 15, 25,
etc. We are now tantalisingly close to
finding the number $r$.
We have set 1 in a state $|x\rangle + |x+r\rangle + |x+2r\rangle + \ldots$ All we need to do now is feed this through the QFT and perform a measurement. Remember, the outcome will be a speed, which is very likely to be close to $k/r$ revolutions per second, where $k$ is a random integer. We can then do some clever guessing and checking on a classical computer to find $k$ and $r$. Once we have $r$, we very easily find a factor of $N$. And we're done! We just hacked into your friend's bank account!
The Art of Sweeping Complexity Under the Rug
You probably have lots of questions. Maybe you're wondering "What actually is this machine you keep talking about?" Or maybe, "How does the QFT actually work in the real world?" Or "Why does this modular exponentiation stuff give us a factor of $N$?" Or maybe just a simple "What?" These questions can be divided into three classes. The first two questions belong to the "I want more quantum details" class. The third belongs to the "I want more classical details" class. And the fourth belongs to the "My brain hurts" class. The solution to the final class of questions is a cup of tea, a break, a think, and then a re-read of everything that's come before. The more you grapple with these ideas the easier everything becomes! The solution to the second class of questions is to watch this YouTube video. He explains everything much better than I ever could. But to give just a teeny bit more explanation, it turns out that if we find the period $r$ to be even, then either $(a^{r/2}+1)$ or $(a^{r/2}-1)$ shares a factor with $N$. And there's already a classical algorithm due to Euclid to find a factor shared by two numbers. So, assuming that common factor is not $N$ itself, we just use that to find one of the prime factors of $N$.
The solution to the first set of questions doesn't really matter! Or at least, it doesn't matter in a sense. Of course, if you're building a quantum computer you actually need to know how to compute modular exponentials and implement a QFT. But if you're interested in whether or not a factoring algorithm is efficient - that is, if it is practical to implement even for large values of $N$ - then you only need to know one thing about each of these procedures: how do their run-times scale with $N$? That is, if I increase the size of $N$, how quickly do the run-times of these components increase? In order to answer this question we need to break up each of these components into the primitive logic gates required to complete it - a complicated task. But broadly speaking, so long as the number of logic gates grows as a polynomial in the number of digits of $N$, you have an efficient algorithm.3 It may not be very good, but it's not catastrophic.
Often, instead of unpacking their nasty insides, we treat these kind of sub-routines, like modular exponentiation and QFTs, as "oracles" which can magically give us the answers we want. This simplifies things A LOT, because the only remaining question that matters is how many times we need to consult each of our oracles. This question probes at what is called the query complexity of an algorithm. In determining whether our algorithm is efficient, it's much easier to ask the question "how does the number of times we must consult the oracles scale with $N$?" than it is to unpack all the inner workings of those oracles and discuss the true run-time of the whole algorithm. As long as they can be implemented efficiently themselves, we don't care about the oracles, and we can sweep all their complicated machinery under the rug.
You of course have to be careful though. With Shor's algorithm we saw a remarkable query complexity: no matter how large our number $N$ was, we only needed to use the modular exponentiation machine and the QFT procedure once each. As far as algorithms go, it doesn't get much better than that. But when you unpack each of these Delphic helpers, it turns out that you need a bit more time than you thought to complete the task. But they are still efficient to implement and so Shor's algorithm winds up being much, much faster than any classical algorithm we know.
You of course have to be careful though. With Shor's algorithm we saw a remarkable query complexity: no matter how large our number $N$ was, we only needed to use the modular exponentiation machine and the QFT procedure once each. As far as algorithms go, it doesn't get much better than that. But when you unpack each of these Delphic helpers, it turns out that you need a bit more time than you thought to complete the task. But they are still efficient to implement and so Shor's algorithm winds up being much, much faster than any classical algorithm we know.
Quantum Speedup
Where did this extra speed come from? What was the key ingredient that provided the extra computational power needed to complete this difficult task? Well in the Shor case, the key ingredients for the algorithm were superposition and interference. We first needed to be able to create superpositions of outputs to the modular exponentiation function. We then changed basis using the Quantum Fourier Transform so that only certain speeds were likely to be measured, while all others became very improbable (remember the blurry clockfaces). We call this phenomenon quantum interference - changing basis in such a way that certain measurable values become very improbable while others become very probable. These were the keys to the speedup from Shor's algorithm. But for a general algorithm, we're not really sure what the key to the speedup is, or whether it will even provide a speedup.
There's a complication in concluding that we truly have a quantum exponential speedup, even in the case of Shor's algorithm. While it's true that the best known classical algorithms for factoring large numbers are pretty close to exponential and not very efficient, there's no proof that somebody couldn't come up with a new one tomorrow that does better. In fact there's no proof that quantum computers can provide an exponential speedup to any task that's currently thought to be inefficient on a classical computer. Complexity theorists, people who study how long or how much space is required to run certain tasks, summarise this with a very short equation whose validity is not yet known: $BQP\neq BPP$.4 The left hand side is basically the set of all tasks that can be completed efficiently by a quantum computer with high probability, and the right hand side is the set of all tasks that can be completed efficiently by a classical computer with high probability. We're not sure yet if these two sets are different.
There is much to be said about this, and we don't have time to discuss all of it. Maybe we'll just finish with two quick points though. The first is a point of practicality. If you've been terrified for your internet security while reading this, don't worry. We are a long way off building a quantum computer that would be able to factor numbers anywhere near big enough to break encryption! Plus, there are many cryptographers around the world right now working on post-quantum schemes to protect our data. We probably have more pressing global problems at the moment than some hypothetical whiz-bang quantum computer posting to Facebook without our permission.
The second point is what these fast quantum algorithms tell us about the world we live in. We can very easily fall down a rabbit hole when we ask these kinds of questions. David Deutsch promotes the idea that quantum computers are better than classical ones because they can draw on the computational power of other worlds - parallel universes - to complete tasks. Does a quantum speedup really lend evidence to the idea of multiple worlds? Maybe, who knows! Furthermore what, if anything, can quantum complexity tell us about physical things happening in the real world? The universe, after all, is a quantum system. Indeed, you might think of it as a quantum computer constantly calculating the next state in its own evolution. That means that certain tasks that cannot be completed efficiently on a quantum computer cannot be completed efficiently in the real world. So perhaps complexity sets the time scale for events taking place in the quantum world every single day. Can the study of complexity really tell us about the speed of physical processes? Maybe, who knows! Finally, if it turns out that $BQP\neq BPP$, there will be quantum processes that are unable to be modeled within the classical world. So what does that say about the prospect of using a classical brain to understand a quantum universe? As Richard Feynman put it, "Nobody understands quantum mechanics." Well maybe there's a reason for that. But until we can be sure, we might as well keep trying.
There's a complication in concluding that we truly have a quantum exponential speedup, even in the case of Shor's algorithm. While it's true that the best known classical algorithms for factoring large numbers are pretty close to exponential and not very efficient, there's no proof that somebody couldn't come up with a new one tomorrow that does better. In fact there's no proof that quantum computers can provide an exponential speedup to any task that's currently thought to be inefficient on a classical computer. Complexity theorists, people who study how long or how much space is required to run certain tasks, summarise this with a very short equation whose validity is not yet known: $BQP\neq BPP$.4 The left hand side is basically the set of all tasks that can be completed efficiently by a quantum computer with high probability, and the right hand side is the set of all tasks that can be completed efficiently by a classical computer with high probability. We're not sure yet if these two sets are different.
There is much to be said about this, and we don't have time to discuss all of it. Maybe we'll just finish with two quick points though. The first is a point of practicality. If you've been terrified for your internet security while reading this, don't worry. We are a long way off building a quantum computer that would be able to factor numbers anywhere near big enough to break encryption! Plus, there are many cryptographers around the world right now working on post-quantum schemes to protect our data. We probably have more pressing global problems at the moment than some hypothetical whiz-bang quantum computer posting to Facebook without our permission.
The second point is what these fast quantum algorithms tell us about the world we live in. We can very easily fall down a rabbit hole when we ask these kinds of questions. David Deutsch promotes the idea that quantum computers are better than classical ones because they can draw on the computational power of other worlds - parallel universes - to complete tasks. Does a quantum speedup really lend evidence to the idea of multiple worlds? Maybe, who knows! Furthermore what, if anything, can quantum complexity tell us about physical things happening in the real world? The universe, after all, is a quantum system. Indeed, you might think of it as a quantum computer constantly calculating the next state in its own evolution. That means that certain tasks that cannot be completed efficiently on a quantum computer cannot be completed efficiently in the real world. So perhaps complexity sets the time scale for events taking place in the quantum world every single day. Can the study of complexity really tell us about the speed of physical processes? Maybe, who knows! Finally, if it turns out that $BQP\neq BPP$, there will be quantum processes that are unable to be modeled within the classical world. So what does that say about the prospect of using a classical brain to understand a quantum universe? As Richard Feynman put it, "Nobody understands quantum mechanics." Well maybe there's a reason for that. But until we can be sure, we might as well keep trying.
Ada in Quantumland
We've only just scratched the surface of what quantum computers can do. The properties they harness - superposition, interference and entanglement - would allow large-scale quantum computers to infiltrate every area of science and technology. They could allow us to understand the intricacies of protein folding or peer into the epicentres of chemical reactions. They could elucidate complicated physics at microscopic scales. They could allow us to develop more effective pharmaceuticals to treat disease, and more efficient batteries to combat the energy crisis. They could provide unique breakthroughs to optimisation problems and the processing of large amounts of data, contributing to everything from decongested cities to more accurate weather predictions.
Once we have them, we could pose many different questions to our new quantum computers. Just as in the early days of computation, we have the power to dictate the future of a new kind of machine. The computer was born out of the desire to calculate certain sets of numbers. It began confined to the world of pure mathematics. It took a visionary mind and more than a century to see the true capabilities of those early symbol processors. Maybe we're also in that same early phase of discovery as Ada Lovelace and Charles Babbage were, only aware of a small fraction of what is possible using quantum technology. Maybe with the right dose of "poetical science," the quantum age can herald a world of not only technical understanding, but also of intrigue and beauty. Only time will tell.
Footnotes
1 You may worry that in order to make this machine, your assistant would have to first look through each card. Then what would be the point in making the machine in the first place? Well, certainly this whole scenario is a bit contrived, but it can still reveal useful properties about quantum computers in relation to their classical counterparts (see discussion of "query complexity"). But you could also imagine that we already know the rule for getting from the light side number to the dark side number, but we still don't know all the dark side numbers. Then you could make the machine, which just follows this rule, without first having to look at all the cards (see "Shor's Algorithm" section).↩
2 If you don't know what a complex number is, don't worry! I explicitly tried not to rely on them for this discussion. But to satiate your curiosity, they form a natural extension to the numbers you already know. They do so by supposing that $-1$ has a square root. Normally when you square any number you get a positive number back, but the complex number $i$ doesn't obey this rule, instead satisfying $i^2 = -1$. Realising that such a number is just as legitimate as $\sqrt{2}$ or $-5$ has many beautiful consequences. Check out this series of YouTube videos for a really nice introduction.↩
3 Polynomial growth, while it may seem fast (think about how quickly $x^8$ explodes as you increase $x$), it's nothing compared with exponential growth. We should all have a pretty intuitive feeling these days of how sickeningly quick exponential growth is, without me even having to mention the C-word. But basically, with an exponential run-time algorithm, if you add an extra digit to $N$, you'd multiply the run-time by some constant factor. For polynomial run-time algorithms, if you multiply the number of digits by a factor, the run-time also gets multiplied by a factor. Even if that second factor is much larger than the first, you're always going to be laughing in comparison to the dreaded exponential run-time. Because of how dramatic exponential growth is, sooner or later, if $N$ creeps past a certain threshold, you'll have to be computing for as long as the universe has been in existence to factor it.↩
4 You might have heard of the more famous equation $P=NP$. While it's very likely that in fact $P\neq NP$, nobody has yet been able to come up with a proof of this inequality.↩
More Information
Ada Lovelace
https://findingada.com/shop/a-passion-for-science-stories-of-discovery-and-invention/ada-lovelace-victorian-computing-visionary/https://www.chattyfeet.com/blogs/chattyfeet-socks-blog/ada-lovelace-facts-first-programmer
http://cs-exhibitions.uni-klu.ac.at/index.php?id=345
https://www.computerhistory.org/babbage/adalovelace/











CASINO | SBDH
ReplyDeleteCASINO. 동두천 출장안마 1. 포항 출장안마 Casino. No Reviews. 구리 출장안마 Get the inside scoop 안성 출장샵 on Casino. View the latest online 용인 출장마사지 casino review & get $20 free in chip