String Theory and Gravity: How To Find Einstein in the Violin Section
If you ask a person on the street what they know about string theory, probably the most common answer (after "absolutely nothing") will be that it's untestable, maybe even unscientific. There hasn't been a single real world prediction produced from that esoteric, hopelessly complicated theory. But on the contrary, if you were feeling cheeky you might say that string theory has made one prediction that is put to the test every single day: what goes up must come down. It predicts the existence of gravity. In fact, it might be the only theory in which the equations of gravity naturally fall into our laps. Moreover, it is one of the only candidates for a theory of quantum gravity - a theory that could explain how gravity operates on subatomic scales. For decades during the 20th Century, some of the smartest people on the planet tried to force gravity to work at these tiny scales, but it refused to play ball. And then along came string theory, in which gravity didn't need to be forced to cooperate, it appeared as a necessary consequence of a few basic assumptions. This fact was absolutely astonishing at the time, and since then, hundreds more physicists and mathematicians have been seduced by those tiny quantum strings. In this post I want to share their amazement with you and try to convince you that, regardless of whether string theory is right, it is a stunning first step towards a theory of quantum gravity.
So we can already explain everything from black holes to fundamental particles. It seems like physics would be finished right? What else is there to talk about? Well there's a problem: our world is quantum mechanical. That means that when we look at nature very closely, things don't just happen in a neat sequence, one step after another. At small scales, objects like electrons or atoms are totally schizophrenic. To put it concisely, everything that could happen to them, does happen to them. All at the same time. This paradoxical behaviour is what makes a theory a quantum one. The standard model is just such a theory. But general relativity is not. This means that it can't describe processes happening on very small scales or very high energies. For instance, it can't tell us what happened at the big bang or what goes on at the centre of a black hole. And in fact if you try to turn general relativity into a quantum theory, it dissolves into a catastrophic soup of infinities - it breaks really badly. Meanwhile, particle physics does better, but still doesn't work if you look at the world at truly tiny scales. So at the smallest scales we have no theory that tells us what is going on. The world of the extremely small is a mystery.1 And that's where string theory comes in.

Even at this early stage gravity is trying to force itself into the picture. If you take a closed loop of string and look at the lowest-frequency vibrations of that string, the particles you find include something called the graviton. The graviton is like the tiniest ripple in spacetime. It's the quantum building block of all curved spacetime. If you put a bunch of gravitons into one patch of space, as they run about in all possible directions as quantum theory says they must, their fuzzy motion can add together to give you any shape to spacetime you like. They can add together to give you a gravitational wave or a black hole or some contorted mess.
Vibrating strings build the spacetime through which they themselves move. It's an elegant cosmic dance. But is this gravity? Well as we said, in order for Sally to have a viable theory of quantum gravity, we require that whatever spacetime the strings build, it satisfies the equation of general relativity, $R_{\mu\nu}=0$, if we zoom out to large scales.
2 For more on this, read Kurt Vonnegut. Slaughterhouse 5, to be precise. In fact, just read it anyway.↩
3 In fact, this isn't a choice. If we instead tried to build the theory with open strings (ones that look like a piece of twine with two ends), we would find that closed strings had to be included in the theory too.↩
4 For all you pedants out there, yes it's true that the colour will influence how light bounces off the ball, which will influence how it rolls very slightly. And maybe differently coloured paints rub against the felt differently, which maybe slows the ball down. But that would all be missing the point. The theory for how the ball rolls across the table is simplified enough that none of that extra stuff matters. And the colour of the ball is a gauge symmetry of that theory.↩
5 If you are at all familiar with general relativity, you might be used to thinking of "flat" spacetime as one devoid of gravity. This is a different notion of flatness. To get a little more technical, a spacetime manifold satisfying the Einstein equation in empty space, $R_{\mu\nu}=0$, is called Ricci flat. Truly flat spacetime (that is, spacetime without gravity), called Minkowski spacetime, is one such Ricci flat manifold, but it is not the only one. The spacetime surrounding a black hole is another Ricci flat manifold. In the article, whenever I refer to "flat" spacetime, I will be talking about Ricci flatness - a spacetime that might be curved, but that satisfies the vacuum Einstein equation.↩
6 You my be wondering, when do we get rid of these fake rulers? When do we set them all equal to the real ones? Well this touches on one of the problems of string theory. For complicated reasons, you can only set the fake rulers equal to the real ones at points infinitely far in the past or the future. For the same reason, in string theory we don't know how to talk about things happening over finite periods of time. If you want to drape some technical words around this fact, the reason for this is that there are "no off-shell quantities" in a theory of quantum gravity, like string theory. It's all rather confusing and difficult to interpret. But this is a big problem for the theory. Consider it added to the list of problems discussed in the next section.↩
We're going to start by discussing just gravity by itself - a challenging enough task! Having laid down those foundations, I'll introduce the big idea behind string theory - that fundamental particles are made up of tiny strands of vibrating string. And from there we will scout out a path towards quantum gravity. What we'll find is that these strings have the special feature that, in a sense that I will explain, size doesn't matter. While in our everyday world, dropping an ant from a large height and dropping an elephant from that same height produce very different results (the ant survives and the elephant goes splat) in the stringy world there is no difference. What we'll end up seeing is that because of this strange indifference to size, without gravity the entirety of string theory would crumble to the ground, shot to death by inconsistencies. Gravity doesn't just work in string theory, its attendance is compulsory.
Setting the Stage
So what is gravity? And why do we need "quantum gravity," whatever that is? We should start by saying that physics works pretty (extremely) well as it stands. It already provides a fundamental description of everything you will encounter in your life, and most things that you won't - from quarks to quasars. This "everything," as it stands, comes in two different categories.
On the one hand, we have a grand edifice of a theory known as the "standard model of particle physics." This provides the bedrock for almost every phenomenon it is possible for you to encounter. It explains why the sun burns, what atoms are made of, why you don't fall through the floor, and it has been experimentally verified to an absolutely insane degree of accuracy. Given its ridiculous success its self-deprecating name, "the standard model," feels a bit inappropriate. "The most amazing whiz-bang model ever" would be a bit better.
On the other hand, we have a theory gifted to us by Einstein and developed by many others, known as the "general theory of relativity." Again, it's hopelessly named (trust me, it's not as boring as it sounds). Despite the word not appearing in its title, general relativity is really a theory of gravity. It tells us why the Earth revolves around the sun, why you are stuck to your seat and it predicts incredibly strange things like black holes and dark energy. This theory has also been rigorously tested, and our understanding of general relativity is what allows the GPS in your phone to determine your location on Earth to such a high degree of accuracy.
So we can already explain everything from black holes to fundamental particles. It seems like physics would be finished right? What else is there to talk about? Well there's a problem: our world is quantum mechanical. That means that when we look at nature very closely, things don't just happen in a neat sequence, one step after another. At small scales, objects like electrons or atoms are totally schizophrenic. To put it concisely, everything that could happen to them, does happen to them. All at the same time. This paradoxical behaviour is what makes a theory a quantum one. The standard model is just such a theory. But general relativity is not. This means that it can't describe processes happening on very small scales or very high energies. For instance, it can't tell us what happened at the big bang or what goes on at the centre of a black hole. And in fact if you try to turn general relativity into a quantum theory, it dissolves into a catastrophic soup of infinities - it breaks really badly. Meanwhile, particle physics does better, but still doesn't work if you look at the world at truly tiny scales. So at the smallest scales we have no theory that tells us what is going on. The world of the extremely small is a mystery.1 And that's where string theory comes in.
Leaving Kansas Behind
Particle physics treats particles as, well, particles. They're just points in space. If you zoom in on a particle, it still looks just as small as when you started. But string theory disagrees. It says that if you zoom really really far into a particle, you'll eventually see a tiny little strand of vibrating string. The building blocks of the universe are treated as strands not dots.
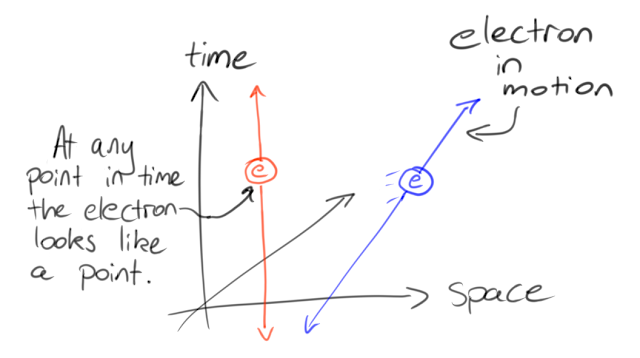
We should introduce a picture needed to make sense of string theory: the spacetime diagram. Let's begin by thinking about things from the point of view of a particle physicist, called Pete (who happens to live in Kansas). Pete, who likes things nice and simple, says that a particle, like an electron, is a point in space. It's just a dot. But while Pete doesn't like things getting too complicated, he has to admit that an electron also has another characteristic feature. It persists in time. If you like, a particle "moves" forward in time, even when it's sitting still in space. We often imagine time as another dimension just like the three that make up space. Bundling time in with the dimensions of space results in a four-dimensional spacetime. If we draw some axes indicating directions in space (e.g. left-right) and directions in time (e.g. towards the future or past) we have a spacetime diagram.
Every point in the spacetime diagram corresponds to, not only a location in space, but also a moment in time. We only indicate two directions in space on the diagram because trying to draw a four-dimensional picture is pretty hard. Now let's see what an electron looks like when we draw it on this diagram. Pete insists that an electron looks like a point in space. But this electron doesn't just exist now. It existed a minute ago and it will exist a minute from now. What that means is that an electron always moves through time. So Pete says that on the spacetime diagram, an electron traces out a vertical line as time ticks forward. This line is called the electron's worldline, so-called because it represents the entirety of the electron's life span. These worldlines represent everything that a particle has done and will do throughout its entire existence. On the figure below, the red vertical line is the worldline for an electron not moving in space. Meanwhile the blue diagonal line is the worldline of an electron that is moving.2
However, Sally the string theorist looks at this picture and says, "Not so fast. I believe an electron is not actually a point in space, but a little strand of string." Sally tells us that in the simplest case, a string looks like a closed loop - a rubber band.3 These loops of string also move through time, just like particles. And in doing so, rather than tracing out a line, they trace out a big hollow tube. Sally draws that process on her own spacetime diagram, which looks something like this:
So a string moving in time makes the shape of a rubber hose - but one in which the rubber is infinitely thin. This tube is called the string's worldsheet. While Pete thinks of particles and their worldlines, Sally thinks of strings and their worldsheets.
Well now that we have the pictures, let's take a concerted step out of Kansas and see what these strings might be telling us. All we need to do to start things off is come up with a rule for how the strings behave. The simpler the rule the better. Sally tells us that her rule is about as simple as it gets: a string gets from point A to point B along the shortest route possible. It's just like how rolling a billiard ball from A to B results in it travelling in a straight line - the shortest path between the two points. But instead, points A and B are in spacetime and are made more complicated by the fact that the string is, well, a string, not a billiard ball. But okay, strings travel in "straight lines" through spacetime. Easy enough to accept.
Sally then admits that she's going to complicate things a little, but all for a good cause. She starts by explaining the 'shortest path' rule in a bit more depth. She tells us that if you take the string along some wild path, the area of the worldsheet becomes large. Meanwhile, if you take it on a direct path between two points, the area of the worldsheet is small. For example in the figure above, the worldsheet on the left has a larger area than the one on the right. So Sally explains that the 'shortest path' in her rule is the one that results in the worldsheet with the smallest area possible. Okay, we say, I guess it's still the same rule so I'm fine with that.
But Sally then says we've got a problem. Problems already? "No, no," she says, "this one's an easy fix." She says that working with the 'shortest path' rule (or 'smallest area' rule) in practice is hard and annoying. What we need to do is change the rule slightly to make it easier to work with. The way that we do this, Sally tells us, is to allow ourselves the freedom to change how we measure areas on the worldsheet. Usually we think of areas as being measured with a ruler - you measure the length and then the height of something, multiply those two numbers together, and that gives you the area. This is no different on the worldsheet - you need a ruler to measure the area (actually you need to slap a ruler down on the worldsheet at each point but don't worry too much about that). But in the original 'smallest area' rule, we were handed a set of rulers by the background spacetime in which the string moved. Those axes on our spacetime diagrams dictated the rulers we had to use. We had no freedom in how we measured the area: we had to live with what we were given.
But what Sally tells us is that we don't want to use the rulers given to us by spacetime. We want to play with our own toys. So instead of using the "correct" rulers, we just pick our own, which might be stretched or warped to be any length we like. It's important to note from the beginning that these new rulers are constructs of our imagination. They don't mean anything. The real rulers are the ones given to us by spacetime. But that's okay, let's use our fake rulers and see what we get. "What we do," says Sally, "is kind of a mathematical trick. We now measure the area using our fake rulers, and then at the end of the whole process, we set our fake rulers to be the same as the real ones. So we allow ourselves some freedom for a moment, and then get rid of that freedom again at the end." This seems like it wouldn't benefit us much, Sally admits. But this extra freedom, even just present during the intermediate steps, helps us a lot. "We should note though," Sally continues as Pete looks like he is going to pipe up, "that this trick is not something that can be done for any object other than a string. The string is special!"

This new-found freedom to change the rulers makes the theory much easier to work with. But, as we said, these rulers aren't real, they're just a mathematical convenience. So changing them doesn't actually change anything physical about the string. The freedom to choose our ruler was just added in by hand to make our lives easier. It would be like in the real world if you decided to measure in inches rather than centimetres - that shouldn't change any of the physical predictions you make. Or, going back to the example of the billiard ball: we had the freedom to change the colour of the ball, but that didn't change how it rolled from point A to point B.
Whenever you can do something to an object that leaves it unchanged, that object is symmetric in some way. For example, if you rotate a square through 90o it looks the same - the square is a symmetric shape. What the previous paragraph is saying is that the worldsheet has symmetry too. It is unchanged when you alter the fake rulers used to measure areas. Now this is a very sacred kind of symmetry. It simply does not make sense for that symmetry to be broken. While I can squash the square into a rectangle so that the 90o rotation symmetry is broken, there's no way that changing the fake rulers on the worldsheet could affect how it moves. How could it? We set them to be equal to the real ones at the end of the calculation! It would be as nonsensical as suggesting the colour of a billiard ball could alter its trajectory. The symmetry comes from the extra freedom we added in by hand, so the theory would be inconsistent - it wouldn't make sense - if it were broken.
Sally then says that we're going to attach some names to these concepts we've been discussing. The type of symmetry associated with changing the size of rulers is called scale invariance - the theory is invariant under changes to length scales. And any symmetry which must be protected in order for the theory to be consistent is called a gauge symmetry. For example, the colour of a billiard ball is a gauge symmetry of the theory for how it rolls around the table. I can change the colour of the ball and there's no way that will influence how it moves.4
Now this scale invariance possessed by the worldsheet is very special. In the day-to-day world, things look very different as you change length scales. Going back to the example briefly mentioned up top, try dropping an ant from a metre up onto the floor. While it might be a bit perturbed, the ant will probably be able to pick itself up and walk off very easily. Now a metre is about 200 times the length of the ant itself. Try dropping an elephant from a height of 200 times its length. It won't be a pretty sight. In this case, physics cares about scale. You can't just scale up the size of the animal and expect the same result.
But in string theory, in the words of Yoda, "size matters not." And this scale invariance, which is unique to a theory of strings, is the key that makes gravity pop out of the maths of the theory. In fact, once we dedicate ourselves to protecting this symmetry, we have no more choices left to make. We are forced to follow the yellow brick road all the way until we reach a theory of quantum gravity.
An Aside: General Relativity
But what are we looking for when we talk about gravity popping out of the maths? Before we go further down the road towards quantum gravity, let's just quickly talk about the non-quantum theory of general relativity (GR). The gist is this: what we call gravity is actually just the result of objects travelling through a curved spacetime. Matter curves the spacetime around it, and conversely, the curvature of spacetime dictates how objects move through it. This already is an extremely mind-bending facet of nature and we'll come back to look at it in more detail in a future post. But all you need to know for now is that gravity is like the curving of a rubber sheet.
Given that this is such a complicated idea, and one that requires pretty complicated set of mathematical tools to properly deal with, it is truly delightful that the entire theory can be expressed in one very succinct equation. In its simplest form in empty space, this equation simply reads: $$R_{\mu\nu}=0.$$
The left-hand side of this equation just represents the curvature of spacetime, and the right-hand side is, well, zero. The equation of GR says that empty spacetime is in some sense not curved (in other words, it is flat). I say "in some sense" because in another sense it is still curved. But we don't need to get too technical.5 Suffice to say, any patch of empty space satisfies the above equation. It's pretty remarkable that such a simple-looking equation can support such complicated solutions as black holes and gravitational waves.
Now, in general, a quantum theory of gravity will be a theory which works on very small scales. We don't know what it might look like on those scales. But on large scales it should look equivalent to bog standard GR. As we blur away the quantumness by zooming out, we expect to reproduce the theory of Einstein. So the reason I wrote down the above equation is because we are going to see it pop up again, within the context of string theory. Strings at large length scales will force GR back on us, without us even having to ask.
Follow the Yellow Brick Road
This theory of strings we have so far is not a quantum one. The first step along the road towards quantum gravity is to turn the strings quantum. As I mentioned, a quantum theory is one in which anything that can happen, does happen. A string travelling from A to B doesn't just go on one path between the two points, it explores all possible paths before ending up at B. If you find that crazy you're not alone. It is crazy. But as strange as it is, it's not impossible. So what happens to Sally's 'shortest path' rule then if the string goes along all paths? Well it gets relaxed a bit. The rule now becomes: the string is most likely to have travelled along the shortest path between A and B. But on which path did it actually travel? Nature forbids you from asking that question.
Let's try to get a picture of how these quantum strings behave. Just like strings on a violin, fundamental strings can vibrate. And again, just like strings on a violin, they can only vibrate at certain frequencies determined by their length. Sally's big idea is that if you look really closely at an electron, you'll find a strand of sting vibrating at a particular frequency. And if you look really closely at a beam of light, you'll find a string vibrating at a different frequency. The frequency with which a string vibrates determines the identity of the object you find when you zoom back out.
Let's try to get a picture of how these quantum strings behave. Just like strings on a violin, fundamental strings can vibrate. And again, just like strings on a violin, they can only vibrate at certain frequencies determined by their length. Sally's big idea is that if you look really closely at an electron, you'll find a strand of sting vibrating at a particular frequency. And if you look really closely at a beam of light, you'll find a string vibrating at a different frequency. The frequency with which a string vibrates determines the identity of the object you find when you zoom back out.
Even at this early stage gravity is trying to force itself into the picture. If you take a closed loop of string and look at the lowest-frequency vibrations of that string, the particles you find include something called the graviton. The graviton is like the tiniest ripple in spacetime. It's the quantum building block of all curved spacetime. If you put a bunch of gravitons into one patch of space, as they run about in all possible directions as quantum theory says they must, their fuzzy motion can add together to give you any shape to spacetime you like. They can add together to give you a gravitational wave or a black hole or some contorted mess.
Vibrating strings build the spacetime through which they themselves move. It's an elegant cosmic dance. But is this gravity? Well as we said, in order for Sally to have a viable theory of quantum gravity, we require that whatever spacetime the strings build, it satisfies the equation of general relativity, $R_{\mu\nu}=0$, if we zoom out to large scales.
Lions and Tigers and Broken Symmetry
At this point Pete smugly pipes up again and tells us that Sally has a problem. Quantum theories, he tells us, are very tricky. Even those that at first appear to be scale invariant almost always turn out to depend on length scale. "Take an electron," he declares. "The particle physics version of the electron, not this stringy nonsense. Just think of it sitting in empty space." Pete goes on to tell us that quantum theory predicts that electrons can interact with particles of light, photons. What that means is that an electron can give a little shiver and spit out a photon, for no reason at all. And if a photon is traveling near the electron, the latter can gobble that photon up, again for no reason at all. In a quantum theory, if something can happen then it does happen. So an electron just sitting there in empty space is constantly emitting photons, and then reabsorbing the ones it has just emitted. It sits in a little halo of light.
In order to move, the electron needs to wade through this cloud of photons. Just like if you tried to wade through treacle, this cloud slows the electron down. It makes the electron harder to set into motion. If something is hard to set into motion, that means it is heavy - things with more mass are harder to accelerate. So the photons make the electron appear heavy. Now if you zoom into the electron, looking at it very closely, these photons seem more sparsely separated and so have less of an effect on the electron. If you give it a very small kick it will move much more freely than it did at larger length scales, and that means the mass you measure will be smaller. Pete summarises: "So the theory of the electron does not have scale invariance, because the mass of the electron changes as you zoom in. And this happens with pretty much all quantum theories. But in your string theory, you need scale invariance. Zooming into the worldsheet is the same thing as stretching the rulers you use, but those rulers are fake, so stretching them cannot change anything physical. So, explain to us, how do your strings retain their precious scale invariance?"
Sally knows that Pete is right. These quantum clouds mean that theories possessing scale invariance can lose that special feature when they are elevated to quantum status. But in string theory this would be catastrophic. The scaling symmetry in string theory isn't something we can get rid of, it's a gauge symmetry. So if it were broken in the quantum theory, the entirety of string theory would be inconsistent. But Sally isn't phased. It actually turns out that avoiding this catastrophe will be the key to finding gravity lurking in the maths.
Meeting the Wizard: Gravity from Strings
Quantum particles look different at different scales. So what about them exactly changes? Well the behaviour of a quantum particle is determined by a set of numbers called couplings. These couplings are the things we think of as being intrinsic characteristics of the object. "That's right," says Pete. "For the electron, the couplings are its charge and mass, for example. The couplings of a particle are the knobs and dials that determine how it moves and how it interacts with its neighbours, and these numbers are the things that change when you zoom in, looking closer at the particle. In the case of the electron, its mass shrinks and its electric charge grows when you probe it at smaller length scales."
The evolution of a coupling is governed by what's called its beta function. This tells you, according to Pete for example, how the mass of an electron changes as you zoom into it. So an electron has one beta function for its mass, and another beta function for its charge. If it turned out that the beta function of an electron's mass was equal to zero, that would mean that its mass would not change as you zoomed in. "Exactly," says Sally. "So, in string theory, if the beta functions are zero, the string doesn't change at all as we zoom in. And if that's the case, the theory has the scale invariance it needs."
So if string theory is to be consistent - if it's not going to be complete nonsense - we have to declare that the beta functions for all the couplings are zero. If we didn't do that, the string would change as we zoomed into the worldsheet. Or in other words, as we altered the fake rulers on the worldsheet. And that would break scale invariance. But what are the couplings of string theory? Strings don't have numbers like charge or mass attached to them - they're too fundamental for those kinds of things.
Now Sally is in the home stretch. "Okay," she says. "Let's set the scene by considering a background patch of spacetime - a stage on which our strings can play. Now if we fill that patch with softly vibrating loops of string, which we said were gravitons, they warp and bend that background spacetime so that it develops some curvature. Next, we'll look at just a single string moving through that background. Let's call him Jerry. We want to consider what happens when we change the fake rulers on Jerry's worldsheet. We know that some couplings may be affected by that change, but what are they exactly? It turns out that the only coupling we're interested in has something to do with the background spacetime."
Okay so changing the rulers on the worldsheet might change something about the background spacetime? "Yes. To see why that's the case, just think about what strings do. They vibrate. But specifically, they can vibrate in any direction. Some part of Jerry might be vibrating left and right and then a moment later switch to vibrating up and down. How often does that switching happen? Well, intuitively, Jerry can only change the way he moves by bouncing off something else in the background patch." Sure, like if you had two jellies, they would have to hit one another to start wobbling. "Um, sure. So if Jerry bounces off another string, that might set him wobbling in a different direction. And the longer we wait, the more likely Jerry is to bounce off another string, just at random. So, if you wait a long time, you see lots of changes to Jerry's vibrations. So kind of weirdly, duration in time is a dial that we can change to alter something about Jerry. In other words duration, the ticking of a clock in the background spacetime, is a coupling for the string."
"Wait," chimes in Pete. "So normally in a quantum theory, if we zoom in, the couplings change. So what you're saying is that we would expect that changing those arbitrary rulers on Jerry's worldsheet would somehow alter the ticks of a clock on the background spacetime?"
"You're not as dumb as you look," says Sally. "That's right. At first glance you would expect: change the rulers and you change the background clock. And you can work out how much you expect those clock ticks to change, and it turns out that the amount of change we expect is given by something we've seen before: the curvature of spacetime, $R_{\mu\nu}$. So if the curvature is large, the background clock changes speed as you zoom in."
"But as you pointed out Pete, we said before that in order for string theory to work, everything must stay the same if we zoom into the worldsheet. The fake rulers we slap onto the worldsheet don't mean anything, so changing them shouldn't do anything to the background clocks. We summarised this by saying that the worldsheet had to have scale invariance. In other words, the amount of change of the clock ticks as we zoom in must be zero. And that amount of change we just said was given by the curvature of spacetime, $R_{\mu\nu}$. If the amount of change is zero, that means $R_{\mu\nu} =0$. The background spacetime has to be flat. But this is exactly the same as the equation of general relativity! By ensuring that string theory doesn't break, we've discovered the existence of gravity!" Sally then takes a bow.
Taking Stock
This is such a beautiful result. Let's retrace the path we took to get here. We started with a theory of strings obeying a simple rule: the string moves along the shortest path between two points. In other words, the string moves in a way that minimizes the area of its worldsheet. But that rule was annoying to work with so we added some extra freedom to the theory by allowing ourselves to change the rulers used to measure areas. We got away with this by setting the fake rulers to be equal to the real ones at the end of it all.6 Then in order for this theory to make sense, we had to maintain that nothing actually physically changed if we used different fake rulers. This fake length scale shouldn't make a difference. We summarised this by saying that the worldsheet was scale invariant. That means, when we promoted it to a quantum theory, we had to make sure all the couplings stayed the same as we zoomed in or out of the worldsheet. We then found out that an important coupling of the string was the clock used to measure background time. So as we zoomed in, this clock had to tick in exactly the same way. However, it turned out that in reality, the clock ticks would change by however much curvature there was in the background spacetime. So the only way that the clock would be unchanged, and that we could maintain scale invariance, is if the background was not curved at all. The only background spacetimes that can be built with strings - the only ones that don't break the theory - are those that satisfy the equation of gravity.
I think you'd be pretty hard pressed to find a result in science that required such extraordinarily minimal input to produce such rich output. The only thing we had to do was decide to focus on lines rather than points (strings rather than particles) and impose a fairly reasonable rule on the behaviour of those lines, and gravity flowed out of the maths as a completely necessary consequence! While it was so difficult from the particle perspective to build a quantum theory of gravity, from the string perspective, it's impossible to get anything else! When people talk about beauty in mathematics, this is a pretty great candidate for what they mean. From one perspective, something seems impossible, while from another, it's perfectly natural. Nature probably thinks we're complete idiots for not having seen it all from the very start.
Behind the Curtain
In the history of 20th Century physics, the discovery of Einstein's equations lurking in the mathematics of quantum strings was a turning point, for better or worse. Depending on who you ask, string theory is either the closest thing we have to a theory of quantum gravity, or it's a complete waste of time that's consumed a generation of physicists. The reason for this controversy is the same reason for the theory's great success: strings are high maintenance creatures. They really are the brats of the quantum world.
If you keep following the maths beyond Einstein's equations, you find many more requirements that strings need in order to be satisfied (that is, in order to preserve the theory's consistency). The scale invariance that was so important for finding gravity, turns out only to be preserved if spacetime has many more dimensions than we see. Specifically, it must have 10 dimensions! No worries, the string theorists say, these extra dimensions must just be too small for us to see and therefore out of our reach, in the same way that a tightrope walker thinks she can only move back and forth, but an ant crawling across the same rope can also move left to right. As you look very closely, there is an extra dimension that presents itself to you.
But then it turns out that the number of ways that you can hide those extra dimensions from view is enormous. And we have no idea how to sort through that huge number of possibilities. That's a big problem, and it also spoils that feeling of inevitability that we had all through our previous journey. Moreover, strings also require something called supersymmetry in order to avoid other potential problems with the theory. But no evidence of supersymmetry has been detected at the LHC or anywhere else.
But probably most troubling of all, nobody actually knows what string theory is. It started out as a theory of strings, hence the name, but it actually might turn out that the string is the wrong place from which to start. If you start from strings, we have no idea how to talk about things that might interest us, like the centres of black holes or the big bang - the primary reasons we were motivated to look at quantum gravity in the first place! And it's not just that the maths is hard, it's that - for complicated reasons - the whole theory is kind of impossible to interpret! It turns out that you probably have to start from somewhere else in order to deal with these extreme environments. String theorists now tend to believe that something called holography might be the key to understanding the true nature of the theory. But that's a story for another day.
But if nothing else, string theory teaches us that gravity is not fundamentally incompatible with quantum theory. It has the ability to present itself to us completely naturally. And this beauty is what entices so many physicists further into the weeds of this strange theory. Maybe in the end, all of this extra confusion will be cleared up and we'll retain a beautiful theory requiring few assumptions. Or perhaps the problems mentioned will turn out to be insurmountable. We'll just have to proceed further up each of our tangled masses of worldsheets to find out. Or in other words, wait and see!
Footnotes
1 It's assumed that our theories of particle physics are just an approximation to something going on at smaller scales. We're not quite sure at which scale exactly these new phenomena will appear. The Large Hadron Collider (LHC) has already probed down to lengths of around $10^{-20}$ metres and found the standard model to work perfectly well. For a sense of perspective, if you blew up a hydrogen atom to be the size of the Earth, the LHC could see objects around the size of a pencil. We think that the absolute smallest length scales are at about $10^{-34}$ metres. This length is called the Planck length. It is much much smaller than anything we've probed with particle accelerators to date. To understand how small the Planck length is, imagine blowing up, not an atom, but a proton to be the size of, not the Earth, but the solar system. If a proton were the size of the solar system, a Planck length would be around the size of a grain of pollen.↩2 For more on this, read Kurt Vonnegut. Slaughterhouse 5, to be precise. In fact, just read it anyway.↩
3 In fact, this isn't a choice. If we instead tried to build the theory with open strings (ones that look like a piece of twine with two ends), we would find that closed strings had to be included in the theory too.↩
4 For all you pedants out there, yes it's true that the colour will influence how light bounces off the ball, which will influence how it rolls very slightly. And maybe differently coloured paints rub against the felt differently, which maybe slows the ball down. But that would all be missing the point. The theory for how the ball rolls across the table is simplified enough that none of that extra stuff matters. And the colour of the ball is a gauge symmetry of that theory.↩
5 If you are at all familiar with general relativity, you might be used to thinking of "flat" spacetime as one devoid of gravity. This is a different notion of flatness. To get a little more technical, a spacetime manifold satisfying the Einstein equation in empty space, $R_{\mu\nu}=0$, is called Ricci flat. Truly flat spacetime (that is, spacetime without gravity), called Minkowski spacetime, is one such Ricci flat manifold, but it is not the only one. The spacetime surrounding a black hole is another Ricci flat manifold. In the article, whenever I refer to "flat" spacetime, I will be talking about Ricci flatness - a spacetime that might be curved, but that satisfies the vacuum Einstein equation.↩
6 You my be wondering, when do we get rid of these fake rulers? When do we set them all equal to the real ones? Well this touches on one of the problems of string theory. For complicated reasons, you can only set the fake rulers equal to the real ones at points infinitely far in the past or the future. For the same reason, in string theory we don't know how to talk about things happening over finite periods of time. If you want to drape some technical words around this fact, the reason for this is that there are "no off-shell quantities" in a theory of quantum gravity, like string theory. It's all rather confusing and difficult to interpret. But this is a big problem for the theory. Consider it added to the list of problems discussed in the next section.↩
Some Sources
- This article on how the electron mass and charge depend on scale was the only one I could find in which the dependence was explicitly stated. A very helpful sanity check!
- This discussion was very helpful for putting into words the reason why scale invariance on the worldsheet is important.
- Cambridge notes on string theory by the inimitable David Tong. Impossible to do without.












It might be worth mentioning that there exist several alternatives to String Theory. Most prominent of them is Loop Quantum Gravity.
ReplyDeleteThanks for your comment! I chose to focus on string theory in this post just for the sake of clarity, but the problems mentioned at the end hint that the alternatives might be more attractive. I'd like to do these other theories justice though, and so hopefully I'll get around to devoting a separate post to LQG, for example.
DeleteThank you for a fantastic post and very pretty illustration. It was a pleasure to read, and I'll definitely keep it bookmarked.
DeleteSorry for a terse initial comment. It was mostly targeted at following sentence: "Moreover, it is one of the only candidates for a theory of quantum gravity". I'm not a native speaker so perhaps this made a wrong impression and you didn't want to say that there are no viable alternative theories to String Theory.
In any case, I'll be happy to answer any questions (or provide pointers since I'm still studying it myself) about LQG. Feel free to reach out if you'll have any.
No problem at all, happy to receive all comments! But I'm very glad you liked the post!
DeleteI'm looking forward to diving into LQG at a later date, and I'll be sure to reach out when I do.
These theories and examples are just so ephemeral and non-concrete. And there are so many levels of assumptions that I don't quite relate with. Ok, first we assume particles are in fact strings. I'm fine with that because it's the starting point. But why do we assume scale invariance? On that topic specifically, initially I understood scale as pertaining to the worldpath of the string. When and why did we drop all other "couplings" as you call them, and only look at time? I wished you would have kept using the wouldpath analogy because that's where we started. Why was that dropped? Duration is actually visible in that diagram. I feel our very understanding of strings is based on an underlying experience of particles. We can't draw anything without particles. I mean, what are the strings made up of, if not particles? How would they be able to vibrate, if there were no local relative undulations in space, which can only be modeled by particles? I was really hoping this article would enlighten me, but it just makes me feel more confused.
ReplyDeleteHi Payton, I'm sorry if this post was more confusing than I intended! Let me see if I can clear some things up. It feels like maybe the things that are most unclear are principally concerned with the rulers and clocks we use to measure distance and duration. If this is the case, let's just add a little more terminology to simplify our discussion. We call the collection of rulers and clocks that measure distance and duration on any manifold, a "metric." Now, we need to distinguish between two different metrics: firstly, there is the one we use to measure distances and durations in the background spacetime, and secondly there is the one we use to measure distances and durations on the worldsheet (the path traced out by the string as it moves).
DeleteNow, normally we would say that these two metrics were the same - measuring distances on the worldsheet would be the same as measuring the distance between the same two points in the background spacetime. But to make progress in string theory you have allow them to be different (this was why in the post I said we introduce "fake" rulers on the worldsheet - the worldsheet metric becomes fake when we allow it to differ from the background metric). And when you do that, the price you pay is that you must have scale invariance on the worldsheet. In other words, the worldsheet metric is fake, so we have to be able to change it without affecting anything physical.
Now the coupling for the string is the real BACKGROUND metric - different to the fake worldsheet metric. The worldsheet picture is still there, it wasn't dropped, but when we discuss couplings, we are talking about a different set of rulers and clocks - those of the background spacetime. The reason I only talked about a background clock in the post (rather than including background rulers in the discussion as well) was just to simplify things a bit, and also for a more technical reason that isn't really important to understand.
So just to summarise: When we talk about scale invariance, we mean changing the worldsheet metric. But changing the worldsheet metric (zooming into the worldsheet) affects the couplings, one of which is the background spacetime metric.
DeleteIn regards to your last point, I'm not sure what you mean by particles in that context? If you mean just points, then yes a string is made up from an infinite number of points. If you want to think of strings in this way, that's totally fine. But usually "particle" means more than that - usually we use the word to refer to things like electrons or photons, under the assumption that they have no internal structure, they are just points in space.
Love your blog though :-)
ReplyDeleteThank you!!
Delete