Codes and Demons: Are Quantum Computers Possible?

"This is not a drill! I repeat, this is not a drill!"

......

There's a strange couple of sentences. If you were an alien, plonked down on Earth with only a dictionary in hand, wouldn't those two exclamations strike you as a bit odd? Why repeat what you have just said, particularly when the content is apparently so urgent? Why use so much redundant waffle?

Well despite what we might think, an alien would probably not find the repetition of an urgent message particularly surprising. The features of information are the same, regardless of the language you speak, whether that be English, Vogon or C++.

The reason for redundancy in language is the presence of noise. Suppose you had one bit of information: a number which might be either valued 0 or 1. And say you wanted to transmit that bit of information to your friend, Alice. But you have to send this bit over a noisy channel. For example, maybe you're sitting in a lighthouse and you flash the light once for "0" and twice for "1." But sometimes there are clouds obscuring the path between you and Alice, or there's a flash of a car headlight from the land that Alice mistakes as your beacon. And so sometimes Alice reads a 0 where you meant to send a 1, or vice versa. Maybe this happens 10% of the time. Well a very natural solution to this problem would be simply to repeat the message several times. Say you and Alice agree beforehand that you will repeat each message three times. Then if Alice sees three double flashes, she thinks it very likely that you wanted to send a 1 (99.9% likely in fact). And if she sees two single flashes and then a double flash she thinks, well you probably wanted to send a 0, but something went wrong on the third flash. So she concludes that your message was "0." Under this strategy of sending the same message three times and taking the "majority rules" vote from the three bits, the likelihood of a miscommunication between you and Alice is 3.1%, which is a fair improvement over the "do nothing" approach, which had a 10% probability of error.

This is pretty intuitive. If you're worried about somebody not being able to hear you, you might repeat what you're saying so that they have a better chance of understanding it. There is a tradeoff between the redundancy of your words and the reliability of your message being transmitted faithfully. Technology utilises this trade-off every day. Computers, hard drives, modems etc. use what are called error-correcting codes to ensure that the messages they want to send, receive, and compute with, are reliable. The "error-correcting code" you used to send signals to Alice with your lighthouse, is called a repetition code. Instead of sending "0," you sent "000," and similarly with "1." In summary, the code you used can be written as: $$0\rightarrow 000, \quad 1\rightarrow 111.$$
Now, you probably know that quantum computers are very different beasts than your run-of-the-mill classical computers. They are governed not by the rules of everyday logic, but by the laws of quantum mechanics. These laws throw a sizable spanner into the works of our simple approach to combating noise. On the one hand, we now have to deal with errors that are infinitesimally small! We somehow have to be able to correct not only the bit-flip errors of classical computers, where 0 is accidentally flipped to 1 and vice versa, but we need to deal with a continuum of possible errors - an infinity of them! On the other hand, quantum mechanics abides by the "No-Cloning Theorem," which dictates that you can't copy your quantum information to make something like the repetition code introduced above. And on the other other hand, whenever you measure quantum information, you destroy it! So how do you even find out if an error has occurred?! Add to all this the fact that qubits are written into tiny systems, whose quantum states are extremely fragile. So errors are almost guaranteed to occur in any realistic device.

These challenges are so profound that, on the face of it, you would be forgiven for concluding that quantum computers are a practical impossibility. It's as if quantum mechanics hides within it a little demon who prevents us from harnessing the theory's potential. I think it's difficult to emphasise how remarkable it is that quantum computers are in fact possible. We can beat the quantum demon. And the path to figuring out how they are possible has led to discoveries with implications throughout physics. Quantum error-correcting codes are strange, fascinating beasts, with properties studied by those interested in everything from bizarre new phases of matter to the nature of space and time. While we will get into these exciting topics in later posts, here I hope to convince you of just this one seemingly trivial fact: quantum codes are possible. And because of that, quantum computers are too.

The Qubit and the Earth

We have discussed in previous posts how to think about the building blocks of quantum computers (qubits). But let's recap this discussion and introduce a different way of thinking about qubits which will prove useful. Qubits are best thought of as little arrows. A normal bit is either a 0 or a 1 and nothing else. But if a 0 is represented by an up arrow, $\uparrow$, and a 1 is represented by $\downarrow$, then a qubit can be, $\uparrow$, $\downarrow$, $\rightarrow$, $\leftarrow$, or anything in between. In general, a qubit is represented by an arrow pointing in any direction in three dimensional space:¹

Whenever we talk about the state of a qubit, we use special brackets. If we want to talk about the state in which the arrow is pointing up, we'll write $|{\uparrow}\rangle$ (or $|0\rangle$, since this state is like the 0 state of a classical bit). The opposite state will be written $|{\downarrow}\rangle$, or $|1\rangle$.

What can we do with qubits? Well, we can use them to store information: changing this information can be thought of as rotating this arrow through space. And what if we want to access the information? Well, using the jargon, we have to make a measurement of the qubit. A measurement involves asking a which-way question. Is the arrow pointing up or down? Left or right? Forwards or backwards? So if we want to make a measurement, we have to first decide which of these questions we are going to ask.

Say we ask the up-down question: Is the qubit pointing up or down? Then the answer we find will be either $\uparrow$ or $\downarrow$ (equivalently 0 or 1) and nothing else. But this seems strange. What if we started with the state $|{\rightarrow}\rangle$? In this case, the arrow's pointing neither up nor down! So how does the question make sense? The answer is that the measurement changes the state of the qubit. If we receive the answer "up," then the state of the qubit spontaneously changes to $|{\uparrow}\rangle$. And if we receive the answer "down," the qubit suddenly pops into the state $|{\downarrow}\rangle$. So if it started in the state $|{\rightarrow}\rangle$, which answer do we receive? Which state does the qubit end up in? Well we don't know for certain. We can only talk about the probability of finding any particular measurement outcome. For the state $|{\rightarrow}\rangle$, each outcome has a 50% probability. So half the time the answer is "up" and the other half of the time the answer is "down."

The probability of getting "up" as your measurement result is determined by how close to being pointed vertically upwards the arrow is. Imagine that the spheres drawn in the cartoons above are little globes of the Earth. The arrow points from the centre to some location on the surface of the globe. If we make an up-down measurement on a qubit whose arrow is pointing at, say, London, then the probability of getting the "up" answer will be quite large, since the arrow is close to the vertical. But if it is pointing somewhere in Antarctica, the answer "up" will be very unlikely. The probability is determined by the orientation of the qubit's arrow.

This picture of an arrow in space is not only useful as a visual aid, but it actually represents the mathematics behind a single qubit very precisely. We've been doing maths without even realising it! Let's delve ever so slightly into that maths. If we want to write down the state of a qubit precisely, we need to start by making a choice, just as we had to do in order to perform a measurement. We need to choose a basis. A basis is just two points on opposite sides of the globe - two poles. If we choose a North and South pole, we can specify any point on Earth relative to those poles (30° N, 40° E - that kind of thing). And similarly with a qubit, if we choose two "poles" we can specify any other state relative to them. We usually choose the $\uparrow$ and $\downarrow$ points to form the basis of our qubit. These points represent the states $|0\rangle$ and $|1\rangle$. Then a general state is written as $a|0\rangle + b|1\rangle$ for some numbers $a$ and $b$. In a sense, if $a$ is large, you can think of the arrow as pointing "more North." And if $b$ is large, the arrow is pointing further into the Southern Hemisphere. Meanwhile if they are roughly the same they are pointing to somewhere along the equator. For example, the state $|{\rightarrow}\rangle$ is the same as $\frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$ when written using this basis.

If we do an up-down measurement on some state $a|0\rangle + b|1\rangle$ we can figure out the probability of getting "up" or "down." The way we find the "up" probability, for example, is by taking the number multiplying the $|0\rangle$ state, so $a$, and squaring it. That (with some caveats) is the probability of getting a 0 if you were to make an up-down measurement of the state. So in $|{\rightarrow}\rangle$, the probability of getting "up" or "0" is $(1/\sqrt{2})^2 = 1/2$, or 50%. Remember, though, we could choose any two poles (any basis) for our measurement. For example, we could do a left-right measurement, and if we did so for the state $|{\rightarrow}\rangle$, we would always find the answer "right" and never "left."

We have discussed in a previous post why these, along with other features of quantum mechanics, allow quantum computers to perform tasks much faster than classical computers can. But in order for them to herald in this new age of ultra-speed, we need to actually be able to store and manipulate the qubits used for computation. Above, I mentioned three grave problems posed to us by the quantum demon. Let's explore each of these in a little more depth.

Three Tricks Up the Demon's Sleeve

Continuous Errors:

What effects might noise have on a stored qubit? Well maybe it might rotate the qubit's arrow to some other point on the globe. We can see that this might influence measurement outcomes: if we start with a state $|{\uparrow}\rangle$, then any up-down measurement could only ever return "up." But if the arrow gets accidentally rotated away from the vertical, an up-down measurement might return "down," where that would have been impossible before. While this probability might be small, these little rotations may add up over time, eventually completely scrambling your information. This rotation-y kind of noise results from a lack of control of your qubit. On the other hand, your information can also be lost if the qubit is jostled by a noisy environment. Basically the environment can "measure" your qubit without your permission, thereby changing its state. Even a stray fragment of light can inflict calamitous damage on a qubit, leaving it in some other unknown state. Alternatively, your qubit's state could "relax" over time, gradually approaching $|0\rangle$, for example. Or you could just lose your qubit altogether!

Many of these noise processes are referred to as decoherence. And if a qubit's state is changed as a result of decoherence, we refer to that as an error. Qubits are horribly susceptible to decoherence. Depending on what approach you use to fabricate a qubit, you may be looking at being able to protect it from errors for only a few milliseconds.

The problem is pretty clear. Not only are qubits susceptible to errors, but the number of potential errors they can suffer from are huge, even infinite! Whereas in classical computers, the only error that could occur is an accidental bit flip, in a quantum computer, any rotation of the qubit's arrow is considered an error. And any slight crack in the protection from decoherence can completely scramble the state of the qubit. What's more, the time taken for this to occur is faster than the blink of an eye!

No-Cloning:

There are many reasons why a repetition code would not be very useful for a quantum computer, but more importantly, a strict repetition code would not be possible, even in principle! Based on our classical intuition, we would assume that we could copy the quantum state of our qubits a whole bunch of times and protect our information in that way. If our qubit were in the state $|\psi\rangle$ (we use Greek letters like $\psi$ to refer to any old, arbitrary quantum state), the repetition code would look something like: $$|\psi\rangle \rightarrow |\psi\rangle |\psi\rangle |\psi\rangle.$$ So this would involve encoding the state of a single qubit into three. But those extra two qubits can't have just appeared out of nowhere, they must have been there from the beginning. We can assume that they began in some other random old state, which we'll call the $|\phi\rangle$ state. So the code actually looks like: $$|\psi\rangle|\phi\rangle|\phi\rangle \rightarrow |\psi\rangle |\psi\rangle |\psi\rangle.$$ But quantum mechanics obeys a very fundamental rule: information must always be conserved. Or, putting it another way, no information can be erased. But in this quantum repetition code, we started with two different states, $|\psi\rangle$ and $|\phi\rangle$, and ended up with only one state, $|\psi\rangle$, copied three times. The state $|\phi\rangle$ was erased and any information about it was lost from the universe. According to quantum mechanics, that is impossible, so a quantum repetition code cannot exist. This is known as the No-Cloning Theorem.

Measurements Change States:

Is there a measurement you could perform to determine state of a qubit? Well suppose we start off with an unknown quantum state, $|\psi\rangle$. How do we get information about it? We need to perform a measurement. So we choose a question to ask (a basis), such as an up-down question, and go ahead and measure the qubit. We find the result 0. Now was that because we started off with the state $|0\rangle$? Or did we start with the state $|{\rightarrow}\rangle$ and get the result 0 just by chance? Or was it $|{\leftarrow}\rangle$, or some other state? All we know was that the initial state was definitely not $|1\rangle$, but that's the only thing we can determine from the measurement. Then after measuring it, the initial state is lost, and we're now left with the state $|0\rangle$. There are no second chances to measure it again.² In summary, it's impossible to recover complete information about a quantum state by measuring it. And that means if we are given only one unknown state, there is no way to determine what it is.

So measurements destroy information. How does this affect error-correction? In the classical repetition code case, if you received a string of bits $010$, you could read off all three bits, notice that the second bit is different from the other two and assume that it had been accidentally flipped. You could then flip it back to correct the error, resulting once again in the string $000$. But in quantum mechanics you're stuck at the first hurdle! You can't even read off a quantum state without altering it, let alone determine what error has occurred! So what can possibly be done?

Foiling the Demon

These problems seem insurmountable but remarkably, they're not. Let's go through them in reverse order.

How do we perform a measurement on a state without destroying it entirely? The answer is to try to obtain incomplete information about the state, by using more than one qubit. Let's see how this works. Imagine you have two sheep, which are each either white or black. Now suppose you ask their farmer a question: "Is the number of white sheep even or odd?" If the answer is even, then you know that either both sheep are white or both are black. And if the answer is odd, then one of them is white but you don't know which. If the colour of both sheep encoded a single classical bit ($0\rightarrow$ both sheep black, $1\rightarrow$ both sheep white), then by asking this "even or odd" question, you may be able to determine whether or not an error has occurred. How? Well you know initially that the number of white sheep is even, regardless of whether the bit encoded is 0 or 1. But if a nefarious criminal steals into the paddock and paints one of the sheep the opposite colour, then the number will be "odd." So receiving the answer "odd" means that the criminal has been through the paddock and tampered with your information. An error has occurred, but we don't know which sheep the criminal painted.

This kind of even-odd type of measurement (called a parity measurement) is fundamentally important in quantum error-correction, since it can provide us with that incomplete information about the qubits that we were seeking. In fact, these measurements can even ascertain what error has occurred and allow us to work out how to correct that error.

Flipping Bits:

But what about the No-Cloning Theorem? How do we get around that? Well instead of repeating the state $|\psi\rangle$ a bunch of times, we can focus on the basis states, $|0\rangle$ and $|1\rangle$. We are allowed to repeat each of these states individually just fine. The No-Cloning Theorem only says that you can't copy an unknown quantum state. If we know which basis state we're dealing with, then we're allowed to copy it. So we will repeat each basis state three times like this: $$|0\rangle \rightarrow |000\rangle, \quad |1\rangle \rightarrow |111\rangle.$$

Okay what does that mean? The key insight is that the three qubits in the above state are entangled. This is a very strange feature of quantum mechanics. If three qubits are entangled like this, it means that they are all pointing in the same direction, up or down, but we cannot know which of these directions it is that they are all pointing in. It's like the qubits have jointly split off into two different branches of possibility: one in which they are all pointing up and one in which they are all pointing down. If you make a measurement, you might find the three qubits in either of these branches. But before doing the measurement, they're all dancing together to an unknown tune. For example, if we have the state $\frac{1}{\sqrt{2}}|000\rangle + \frac{1}{\sqrt{2}}|111\rangle$, there exists one branch in which all qubits are in the $|0\rangle$ state, and one branch in which they are all in the $|1\rangle$ state. And there's a 50% chance of finding the qubits in either of these branches if we were to make a measurement.

This code is okay, but it's not great. It's not able to combat the continuum of errors just yet, but it can correct errors that flip one of the qubits: $|0\rangle \leftrightarrow |1\rangle$. For this reason it is like the classical repetition code and we call it the bit-flip code. How do bit-flip errors affect the state of the three qubits? Let's say we start with the state $a|000\rangle + b|111\rangle$. If the first qubit is flipped, we need to change its value ($0\leftrightarrow1$) in both of those sets of funny brackets (bit flip errors affect all states in the sum in the same way). So we end up with the state $a|100\rangle + b|011\rangle$.

Now remember, we don't know if one of these errors has occurred to our qubits. In order to detect and correct these bit-flip errors, we can perform our parity measurements: we ask, for all pairs of qubits, is the number of 0's even or odd? So let's see what answers we get. We first ask for the parity of 0's between qubits 1 and 2. For example, with the error state $a|100\rangle + b|011\rangle$, in both sets of brackets ($|100\rangle$ and $|011\rangle$) the parity of 0's between the first two qubits is odd. We have the case of one white sheep and one black sheep but we don't know which is which.³ After that, we similarly ask about the parity of 0's between qubits 2 and 3. In this case, for both sets of brackets, there is an even number of 0's between the last two qubits. So that's the answer we receive.

So in total we make two measurements, which come back respectively "odd" and "even." Instantly we can tell that something has gone wrong. If no bit-flip error had occurred, we would have received the answers "even" and "even." So there are now two possibilities: either one or two qubits have been flipped. In order to correct the error, we assume only one qubit has been flipped, since that is the more likely option. This is the same assumption we make with the classical repetition code. With that assumption and a little bit of thought, we can convince ourselves that if we get back the results "odd" and "even" it must have been the first qubit that was flipped: the first result, "odd," tells us that one of qubits 1 and 2 was flipped, while the second result, "even," tells us that neither of qubits 2 and 3 were flipped. So qubit 1 is the culprit. Similarly if we got "odd" and "odd," qubit 2 would have been flipped, and if we got "even" and "odd," it would have been qubit 3.

After diagnosing the bit-flip error, we simply change the qubit that was flipped back to its original value. And in doing so we restore the three qubits to the original state, $a|000\rangle + b|111\rangle$! This procedure has allowed us to circumvent Problems 2 and 3 mentioned above: we have foiled the No-Cloning theorem and we have learnt how to perform measurements that don't destroy our information.

Flipping Signs:

But this isn't yet full quantum error-correction. What happened to that infinity of errors we were talking about? The solution to Problem 1 involves something called discretization of errors. It turns out that we can use the rules of quantum mechanics in our favour to break up that continuum of possible mistakes into a discrete set, simply by performing the parity measurements we've been talking about! In fact, while it seems like the bit-flip code would be useless, because it can only correct one type of error out of infinitely many possible ones, it turns out that it is actually already half way to the goal of full error correction. All we need is the ability to fix one other type of error. A code that can fix both types can actually, miraculously, correct any possible error!

This second type of error is called a phase flip. This occurs when the sign out the front of the $|1\rangle$ state is changed. So, for example, it sends $a|0\rangle + b|1\rangle \rightarrow a|0\rangle - b|1\rangle$. The way of thinking about this error using the qubit arrows is that it flips $|{\rightarrow}\rangle$ to $|{\leftarrow}\rangle$. Why? Remember that we can write the state $|{\rightarrow}\rangle$ using our "North and South poles" as $\frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$. Similarly, we can write $|{\leftarrow}\rangle$ using these basis states as $\frac{1}{\sqrt{2}}|0\rangle - \frac{1}{\sqrt{2}}|1\rangle$. That extra minus sign changes between the left and right states. So while a bit-flip error swaps up and down, phase flip errors swap left and right.

We can quite easily construct a code that protects against phase flips in just the same way as we constructed the bit-flip code. At this point, instead of writing $|{\rightarrow}\rangle$, I'm going to use the common notation and write $|{+}\rangle$ (referencing that all-important $+$ sign). And instead of writing $|{\leftarrow}\rangle$ I'll write $|{-}\rangle$. So now the code that protects against phase flip errors, given the creative name of the phase-flip code, is: $$|0\rangle \rightarrow |{+++}\rangle, \quad |1\rangle \rightarrow |{---}\rangle.$$

Pretty similar to the bit-flip code. And again, an arbitrary state is encoded as $a|{+++}\rangle + b|{---}\rangle$. A phase-flip error changes $|{+}\rangle\leftrightarrow |{-}\rangle$ and so, if such an error occurs on the first qubit, it will result in the state $a|{-++}\rangle + b|{+--}\rangle$. By asking questions like "is the number of $+$'s between the first two qubits even or odd?" etc. we can correct these errors in just the same way as before.

Discretization of Errors:

So I've told you that if we can fix bit flips and phase flips, then we can fix any arbitrary error. How could this possibly be? The answer comes from understanding discretization, which is a concept we mentioned earlier. Let's go back to the arbitrary state we've been working with so far: $a|0\rangle + b|1\rangle$. Remember that the arrow of a qubit in this state is neither pointing up or down, but if we make a measurement, the qubit pops into one of these states, chosen at random.

We say that this qubit is in a superposition of the states $|0\rangle$ and $|1\rangle$. In a superposition there are two branches of possibility (arrow pointing up or down), and one of those is picked to be reality, totally at random, when we perform a measurement. Is there a way we could write an error as a superposition of a discrete set of elements too? The answer is yes! Any change to your quantum state can be thought of as a superposition of: no change, a bit-flip error, a phase-flip error, and a combination of the two. That is, after any possible error has occurred to your qubit, the resulting state splits into four possible branches:

Just as in the case of a qubit's state, making the right kind of measurement forces the universe to choose which branch of possibility it wants to inhabit. The case of errors is no different. If we perform the right measurement, the above superposition will collapse into one of those four possibilities: no change, bit-flip, phase-flip or both flips. And the measurements that do the trick are the parity measurements we've already talked about! By performing these measurements, we split up that infinite scary continuum of errors into just four possibilities! This is what we call discretizing the errors.

The upshot is, if we know how to correct bit-flip and phase-flip errors and we can perform parity measurements, we have all the tools we need to correct any possible error occurring on one of our qubits! We've solved the impossible problems posed by the quantum demon.

Our First Quantum Code

While we've discovered that good quantum codes are in theory possible, we still need to find a code that can fix both bit-flip and phase-flip errors at the same time. We have seen two codes that can perform each of these feats separately, so might there be a way to combine them to get the advantages from both?

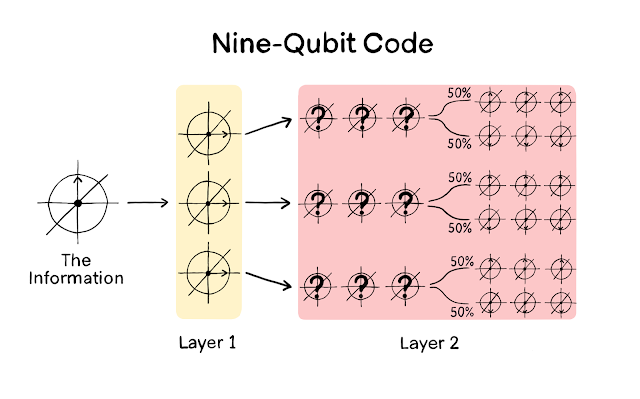
In fact there is. We can use both codes at once. What we're going to do is start with a phase-flip code: $|0\rangle \rightarrow |{+++}\rangle$, $|1\rangle \rightarrow |{---}\rangle$. If we started with the state $|0\rangle$, we now have three qubits, all in the $|+\rangle$ state. This is the first layer of the code, but we're going to go one deeper. To get to Layer 2, we're now going to replace each of these three qubits with another three qubits, encoding the $|+\rangle$ state using a bit-flip code. Down at Layer 2, we have nine qubits, broken up into three blocks of three. And each block of three is in the state $\frac{1}{\sqrt{2}}|000\rangle + \frac{1}{\sqrt{2}}|111\rangle$ (which represents the state $|{+}\rangle$ from Layer 1). The example of using this code to store the $|0\rangle$ state is shown below:

As shown in the picture, down at Layer 2 each block of three is entangled so that there's a 50% probability that they are all pointing up, and a 50% probability that they are all pointing down. In the same way, the $|1\rangle$ state is encoded using the phase-flip code as $|{---}\rangle$ (Layer 1), then each $|-\rangle$ state is encoded using a further three qubits as $\left(\frac{1}{\sqrt{2}}|000\rangle - \frac{1}{\sqrt{2}}|111\rangle\right)$ (Layer 2), where again, there's a 50-50 chance that the qubits are all pointing up or down.

Okay, that was a bit complicated. But we can de-confuse ourselves by trying to understand how this code works. In order to convince ourselves that it can correct both bit-flip and phase-flip errors, let's imagine we are encoding the $|0\rangle$ state, and a bit-flip error occurs on the first qubit. After this error, the first block of three qubits is in the state $\frac{1}{\sqrt{2}}|100\rangle + \frac{1}{\sqrt{2}}|011\rangle$ (this was the same state that we saw with the bit-flip code). Meanwhile the states of the other two blocks are unchanged. We can correct this error in the same way that we did before: by comparing the parity of 0's between the three qubits. These measurements tell us that an error has occurred, and that that error is most likely the first qubit which has flipped. The story is the same if a bit-flip occurs on any of the other eight qubits. We can correct the error so long as only one qubit is flipped. What about a phase-flip? Well suppose this type of error affects the first qubit again. This would mean that a minus sign appears in front of the first qubit's $|1\rangle$ state, which results in the state of the entire first block becoming $\frac{1}{\sqrt{2}}|000\rangle - \frac{1}{\sqrt{2}}|111\rangle$. If we go back up to Layer 1, this state in the first block represents $|-\rangle$. But again the second two blocks are unaffected, both representing $|+\rangle$ states. So at the level of Layer 1, all nine qubits are encoding $|{-++}\rangle$. By checking the parity of $+$'s between the three blocks, we can determine that the first block has been flipped to $|-\rangle$. We can then flip this block back to the $|+\rangle$ state, thereby correcting the error!

And just to drive home the point, since we can use this code to correct bit-flip and phase-flip errors simultaneously, we have actually created a quantum code that can be used to detect and correct the entire continuum of errors that might affect a qubit! These parity measurements within and between blocks not only allow us to fix two types of errors, they collapse a superposition of errors into just one, picked at random. We have beaten the quantum world using its own rules!

Summarising the Hack

Why did this work? The key ingredient we needed in order to correct those two key types of errors simultaneously was enough space. Not physical space, but an abstract space of possible states. All the possible "error states" that could result from a bit flip or a phase flip in our code had to be able to "fit" into the space of possible states. And this could only happen because we had enough qubits in the code to start with. In fact, it turns out that there is no way to build a working quantum code using fewer than five qubits, which is why the bit-flip and phase-flip codes, which each used three qubits, were never going to work perfectly by themselves.⁴

But we can do better than the nine-qubit code introduced in the previous section. There exist small codes, using only five qubits, or large codes, using dozens of qubits, that can correct errors affecting many of them. And there are other features of codes that we might care about, where we can continue to find improvements. In fact, not only can we use quantum codes to protect the intricately delicate information that inhabits the quantum world, but we can use them to manipulate that information as well. We can use them to build a quantum computer.

Being able to store qubits is only part of the challenge of developing a working quantum computer. We must also be able to apply logic gates to the qubits and read out their information. Namely, we need to be able to run quantum algorithms on the device. It seems like the problems we faced for storing qubits will have to be tackled yet again in order to be able to manipulate them. What if we try to perform a logic gate, which might involve rotating a qubit's arrow around to some other orientation, but we accidentally rotate it a bit too much or too little? The sensitivity of the quantum world is coming back to bite us yet again!

But fear not. Just as we can find good quantum codes, so too can we find good ways of manipulating the information that they store. In fact it can be proved mathematically that all the operations making up a working quantum computer can be potentially faulty, and we can still beat the quantum world. So long as the probability of anything going wrong isn't too high, everything works out just fine. Errors and faults can be fixed faster than they are created. Remarkably, without even having to touch a piece of experimental equipment, we can work out that quantum computers are possible, even without the unreasonable levels of precision that we at first expect to be necessary. The quantum demon has well and truly been foiled!

Let's take a look at what we've achieved here. Quantum states are incredibly fragile. The fact that we live according to the laws of classical physics, rather than quantum physics, is proof of that fragility. The quantum world disintegrates into our own at large enough scales and levels of complexity. But despite this, the super-fine manipulations required for quantum computation are not impossible to perform securely. Even with noise and faulty components, we can still in principle build working quantum computers. That's incredibly surprising! Nature could just as easily have gone the other way - quantum mechanics may have been such that no error-correcting codes could exist, or that our gates and measurements had to be perfect. But luckily for us, we are permitted the chance to control the quantum world.

......

I hope you found this first little peek at quantum error-correction interesting! It's a complex topic, but one that I think is very exciting. Quantum codes have progressed a long way since when they were first discovered to be possible, and I'm hoping to delve into these newer discoveries in the near future. To start off with, in an upcoming post we'll look at topological quantum codes. These are codes in which the difference between a ball and a doughnut is precisely the same as the difference between a useless code and a powerful one!

Footnotes

¹ It should be emphasised that this is an abstract picture of the mathematical content of a qubit. There's no physical reality to this arrow.^↩
² If you are quite perceptive, you might notice that what I'm saying here seems to contradict what I said about no-cloning. Measurements destroy quantum information, even though I said that was impossible! Well measurements don't necessarily obey the same laws as the rest of quantum mechanics - in particular, they are not reversible (although this is a controversial topic, and deserves much more time than we have here). But the trade off is that the results of measurements are random. The upshot is that a repetition code is still not possible, even with measurements.^↩
³ Notice that the answer given by both sets of brackets is the same: the parity is odd. This is important, because it means that the measurement we perform in this case does not change the state of the qubits. If the answers between brackets were different, the measurement would change the state, and we would receive only one of the possible answers back, chosen at random.^↩
⁴ This comes from the general result known as the Quantum Hamming Bound. Unfortunately it's not as simple as I've made it out to be. In particular, degenerate quantum codes, can have error states that overlap in the space of possibilities, so they can pack everything in more densely. But it's still the case that you're probably not going to be able to do that much better. 5 qubits is still the minimum needed for a useful quantum code as far as we know.^↩

References

The book Quantum Computation and Quantum Information by M. Nielsen and I. Chuang has everything that I needed for this post. It's really a one-stop shop!

Search This Blog

Campbell McLauchlan